Cho hàm số y = f(x) xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện sau: f ( x ) > 0 , ∀ ∈ ℝ f ' x = - e x . f 2 x , ∀ ∈ ℝ f 0 = 1 2
Tính giá trị của f(ln2)
A. ln 2 + 1 2
B. 1 4
C. 1 3
D. ln 2 2 + 1 2
PB
Những câu hỏi liên quan
Cho hàm số y f(x) xác định và liên tục trên
ℝ
thỏa mãn đồng thời các điều kiện sau: f(x) 0 với
∀
x
∈
ℝ
,
f
(
x
)
-
e
x
.
f
2
x
với
∀
x
∈
ℝ
f
0
1
2...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện sau: f(x) > 0 với ∀ x ∈ ℝ , f ' ( x ) = - e x . f 2 x với ∀ x ∈ ℝ f 0 = 1 2 . Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x 0 = ln 2 là:
A. 2 x + 9 y - 2 ln 2 = 0
B. 2 x - 9 y - 2 ln 2 + 3 = 0
C. 2 x - 9 y + 2 ln 2 - 3 = 0
D. 2 x + 9 y - 2 ln 2 - 3 = 0
Đáp án D
Ta có f ' x = - e x . f 2 x ⇔ - f ' x f 2 x = e x ⇔ ∫ - f ' x f 2 x d x = ∫ e x d x ⇔ 1 f x = e x + C
Mà f 0 = 1 2 ⇒ 1 f 0 = e 0 + C ⇔ C + 1 = 2 ⇒ C = 1 → f x = 1 e x + 1
Do đó f ' x = - e x e x + 1 2 ⇒ f ' ln 2 = - 2 9 . Vậy phương trình tiếp tuyến là 2 x + 9 y - 2 ln 2 - 3 = 0 .
Đúng 0
Bình luận (0)
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Cho hàm số y f(x) xác định và liên tục trên
ℝ
{
0
}
thỏa mãn:
x
2
f
2
(
x
)
+
(
2
x
-
1
)
f
(
x
)
x
f
(
x
)
-
1
đồng thời
f...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên ℝ \ { 0 } thỏa mãn: x 2 f 2 ( x ) + ( 2 x - 1 ) f ( x ) = x f ' ( x ) - 1 đồng thời f ( 1 ) = - 2 Tính ∫ 1 2 f ( x ) d x
LP
4 tháng 3 2023 lúc 18:13
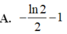
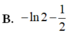
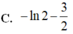
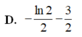
1. Chứng minh rằng mọi hàm \(f:ℝ\rightarrowℝ\) thỏa mãn \(f\left(xy+x+y\right)=f\left(xy\right)+f\left(x\right)+f\left(y\right),\forall x,y\inℝ\)
2. Xác định tất cả các hàm số \(f\) liên tục trên \(ℝ\) thỏa mãn điều kiện \(f\left(2x-y\right)=2f\left(x\right)-f\left(y\right),\forall x,y\inℝ\)
Cho hàm số f(x) có đạo hàm xác định, liên tục
[
0
;
1
]
đồng thời thỏa mãn các điều kiện
f
0
-
1
và
f
x
2
f
x
.
Đặt
T
f
1
-
f...
Đọc tiếp
Cho hàm số f(x) có đạo hàm xác định, liên tục [ 0 ; 1 ] đồng thời thỏa mãn các điều kiện f 0 = - 1 và f ' x 2 = f ' ' x . Đặt T = f 1 - f 0 hãy chọn khẳng định đúng?
A. - 2 ≤ T < - 1
B. - 1 ≤ T < 0
C. 0 ≤ T < 1
D. 1 ≤ T < 2
Cho hàm số y f(x) xác định và liên tục trên R thỏa mãn đồng thời các điều kiện sau:
f
x
0
∀
x
∈
R
,
f
x
-
e
x
.
f
2
x
∀
x
∈
R
và
f
0
1
2
....
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên R thỏa mãn đồng thời các điều kiện sau: f x > 0 ∀ x ∈ R , f ' x = - e x . f 2 x ∀ x ∈ R và f 0 = 1 2 . Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x 0 = ln 2 là:
A. 2 x + 9 y - 2 ln 2 - 3 = 0
B. 2 x - 9 y - 2 ln 2 + 3 = 0
C. 2 x - 9 y + 2 ln 2 - 3 = 0
D. 2 x - 9 y - 2 ln 2 - 3 = 0
Cho biết yf(x) là hàm số liên tục và xác định trên R|{1;3} và thỏa mãn đồng thời các điều kiện:
f
(
x
)
1
(
x
-
1
)
(
x
-
3
)
;
f
(
0
)
2
f
(
2
)...
Đọc tiếp
Cho biết y=f(x) là hàm số liên tục và xác định trên R|{1;3} và thỏa mãn đồng thời các điều kiện: f ' ( x ) = 1 ( x - 1 ) ( x - 3 ) ; f ( 0 ) = 2 f ( 2 ) = 4 f ( 4 ) = 4 Khi đó giá trị của biểu thức: f ( - 1 ) + f 3 2 + f 9 2 nằm trong khoảng?
A . 5 - 1 2 ln 7 18
B . 7 - 1 2 ln 7 18
C . 2 + 1 2 ln 7 18
D . 3 + 1 2 ln 7 18
Cho hàm số
y
f
x
có đạo hàm liên tục trên R, thỏa mãn các điều kiện
f
x
0
∀
x
∈
ℝ
,
f
x
+
3
x
x
-
2
f
x
0
...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên R, thỏa mãn các điều kiện f x > 0 ∀ x ∈ ℝ , f ' x + 3 x x - 2 f x = 0 ∀ x ∈ ℝ và f 0 = 5 . Giá trị của f(2) bằng
A. 5 e 4
B. 5 e - 12
C. 5 e 6
D. 5 e 16
Cho hàm số y f (x) xác định và liên tục trên
ℝ
, thỏa mãn
f
x
5
+
4
x
+
3
2
x
+
1
với mọi
x
∈
ℝ
. Tích phân
∫
-
2
8
f
x...
Đọc tiếp
Cho hàm số y = f (x) xác định và liên tục trên ℝ , thỏa mãn f x 5 + 4 x + 3 = 2 x + 1 với mọi x ∈ ℝ . Tích phân ∫ - 2 8 f x d x bằng:
A. 10.
B. 2.
C. 32 3
D. 72
Đáp án A
Ta có:
⇒ f x 5 + 4 x + 3 = 2 x + 1 ⇒ ∫ - 1 1 5 x 4 + 4 . f x 5 + 4 x + 3 d x = ∫ - 1 1 5 x 4 + 4 . ( 2 x + 1 ) d x ⇔ ∫ - 2 8 f ( t ) d t = ∫ - 1 1 ( 10 x 5 + 5 x 4 + 8 x + 4 ) d x
Đúng 0
Bình luận (0)