Cho đường thẳng ∆ có phương trình tham số là x = − 1 + 4 t y = 3 − 2 t . Phương trình nào sau đây là phương trình tổng quát của ∆?
A.x – 2y + 5 = 0
B.x + 2y – 11 = 0
C.x + 2y – 5 = 0
D.x – y = 0
Đường thẳng (d) có phương trình tham số: x = 2 - 3 t y = 1 + t Phương trình tổng quát của đường thẳng (d) là
A. x+3y+5=0
B. -3x+y-7=0
C. -3x+y+5=0
D. x+3y-5=0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = - 3 t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = 3 - t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình tham số là x = - 1 + 3 t y = 2 - t . Phương trình tổng quát của d là:
A. 3 x - y + 5 = 0
B. x + 3 y = 0
C. x + 3 y - 5 = 0
D. 3 x - y + 2 = 0
Đường thẳng d có phương trình chính tắc x + 1 - 3 = y - 2 1 .Phương trình nào sau đây là phương trình tham số của d?
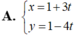

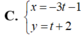
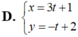
Đường thẳng d có ![]() và đi qua điểm M(-1; 2)
và đi qua điểm M(-1; 2)
Vậy phương trình tham số của đường thẳng 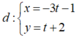 .
.
Chọn C.
Cho đường thẳng d có phương trình y=(3m+1)x-6m-1 m là tham số Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng d là lớn nhất
Lời giải:
ĐK: $3m+1\neq 0$
Gọi $A,B$ lần lượt là giao điểm của $(d)$ với $Ox,Oy$
Vì $A\in Ox$ nên $y_A=0$
$y_A=(3m+1)x_A-6m-1=0$
$\Rightarrow x_A=\frac{6m+1}{3m+1}$
Vậy $A(\frac{6m+1}{3m+1},0)$
Tương tự: $B(0, -6m-1)$
Gọi $h$ là khoảng cách từ $O$ đến $(d)$
Khi đó, theo hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}$
$=\frac{1}{|x_A|^2}+\frac{1}{|y_B|^2}$
$=\frac{(3m+1)^2}{(6m+1)^2}+\frac{1}{(6m+1)^2}$
$=\frac{(3m+1)^2+1}{(6m+1)^2}$
Để $h$ max thì $\frac{1}{h^2}$ min
Hay $\frac{(3m+1)^2+1}{(6m+1)^2}$ min
Áp dụng BĐT Bunhiacopxky:
$[(3m+1)^2+1][2^2+(-1)^2]\geq [2(3m+1)+(-1)]^2=(6m+1)^2$
$\Rightarrow 5[(3m+1)^2+1]\geq (6m+1)^2$
$\Rightarrow \frac{1}{h^2}\geq \frac{1}{5}$
Giá trị này đạt tại $\frac{3m+1}{2}=\frac{1}{-1}$
$\Leftrightarrow m=-1$
Cho đường thẳng ∆ đi qua điểm M 2 ; 0 ; - 1 và có vectơ chỉ phương a → = 4 ; - 6 ; 2 . Phương trình tham số của đường thẳng là:
A. x = 2 + 2 t y = - 3 t z = - 1 + t
B. x = - 2 + 4 t y = - 6 t z = 1 + 2 t
C. x = 4 + 2 t y = - 6 - 3 t z = 1 + t
D. x = - 2 + 2 t y = - 3 t x = 1 + t
Cho đường thẳng d có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 2 + 2t\end{array} \right.\)
a) Lập phương trình tổng quát của đường thẳng d.
b) Tìm toạ độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.
c) Đường thẳng d có đi qua điểm M(-7; 5) hay không?
a) Xét phương trình tham số của d: \(\left\{ \begin{array}{l}x = - 1 - 3t\left( 1 \right)\\y = 2 + 2t\left( 2 \right)\end{array} \right.\).
Lấy \(\left( 1 \right) + \frac{3}{2}.\left( 2 \right) \Rightarrow x + \frac{3}{2}y = 2 \Rightarrow 2x + 3y - 4 = 0\)
Vậy phương trình tổng quát của đường thẳng d là: \(2x + 3y - 4 = 0\)
b) Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{4}{3}\\x = 0\end{array} \right.\) . Vậy giao điểm của d với trục Oy là: \(A\left( {0;\frac{4}{3}} \right)\)
Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 2\end{array} \right.\) . Vậy giao điểm của d với trục Ox là: \(B\left( {2;0} \right)\)
c) Thay tọa độ điểm \(M\left( { - 7;{\rm{ }}5} \right)\)vào phương trình đường thẳng d ta có: \(2.\left( { - 7} \right) + 3.5 - 4 \ne 0\)
Vậy \(M\left( { - 7;{\rm{ }}5} \right)\)không thuộc đường thẳng d.