Sử dụng tổn 3 góc tam giác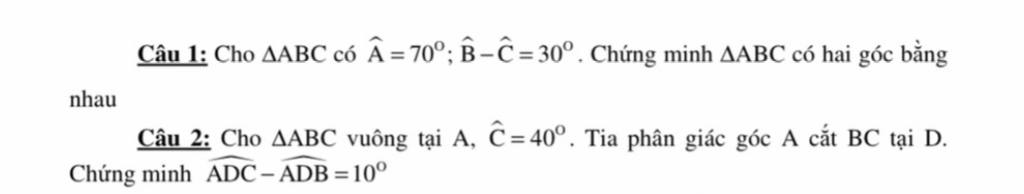
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Sử dụng tổng 3 góc tam giác
Sử dụng Tổng 3 góc của tam giác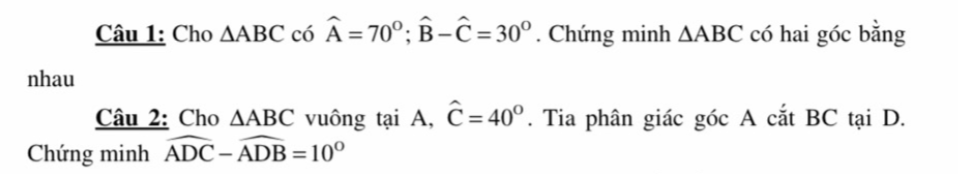
Câu 1:
\(\widehat{B}+\widehat{C}=110^0\)
\(\Leftrightarrow\widehat{B}=70^0;\widehat{C}=40^0\)
Vậy: ΔABC có hai góc bằng nhau
Đúng 0
Bình luận (1)
Trình bày( sử dụng tổng 3 góc tam giác) ạ
Câu 1:
\(\left\{{}\begin{matrix}b-c=30\\b+c=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\c=40\end{matrix}\right.\)
Vậy: ΔABC có hai góc bằng nhau
Đúng 0
Bình luận (0)
Sử dụng tc góc trong, góc ngoài, tổng 3 góc tam giác ạ. Gợi ý cái nào lm trc cx đc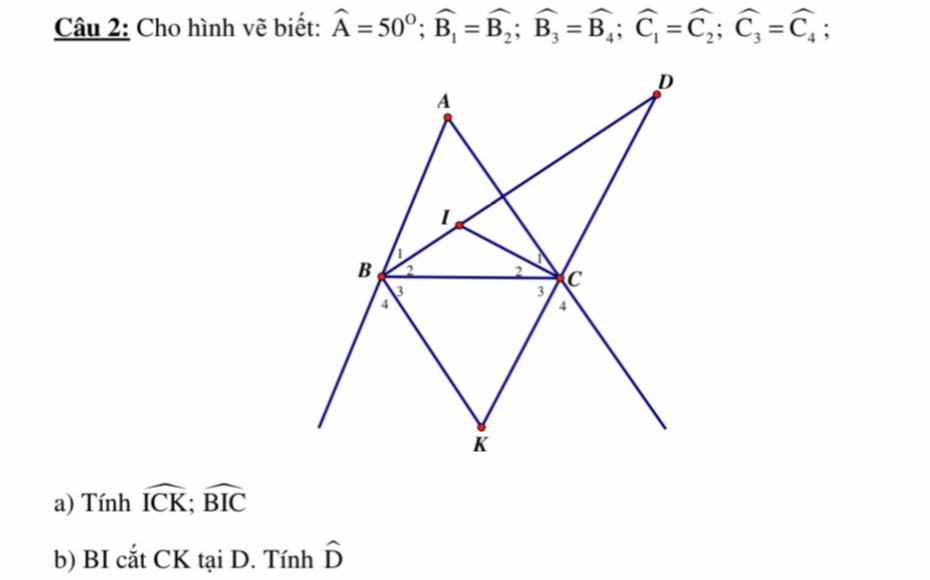
a. Gợi ý: \(\widehat{ICK}=\widehat{C_2}+\widehat{C_3}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{C}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
\(\widehat{BIC}=180^0-\left(\widehat{B_2}-\widehat{C_2}\right)=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-90^0+\dfrac{1}{2}\widehat{BAC}=90^0+25^0=115^0\)
b. \(\widehat{ICK}=\widehat{D}+\widehat{CID}\Rightarrow\widehat{D}=90^0-\widehat{CID}=90^0-\left(180^0-\widehat{BIC}\right)=...\)
Đúng 0
Bình luận (0)
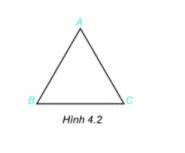
Cho tam giác đều ABC như hình 4.2.
1. Gọi tên các đỉnh, cạnh góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Đúng 1
Bình luận (0)
Sử dụng tổng 3 góc trong tam giác( gợi ý chi tiết cx đc ạ)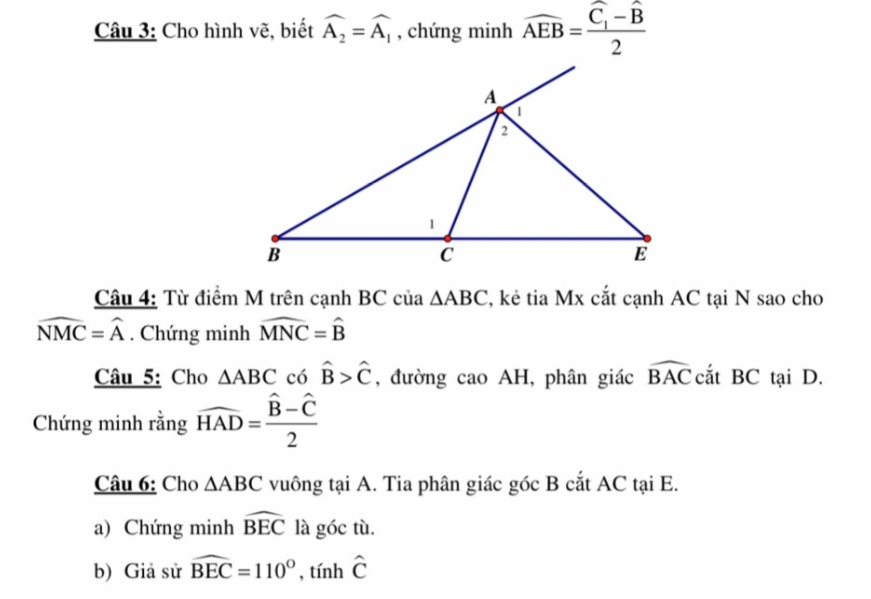
Cho tam giác ABC và tam giác MNP có AB=MN, AC=MB, góc A = góc M. cmr : tam giác ABC=tam giác MNP ( ko sử dụng trường hợp cạnh góc cạnh nha )
Cho tam giác ABC và tam giác MNP có AB=MN, AC=MB, góc A bằng goc M. cmr : tam giác ABC băng tam giác MNP ( ko sử dụng trường hợp cạnh góc cạnh)
chtt nha bạn hiền tick mk nha bạn tốt
Đúng 0
Bình luận (0)
chtt không có đâu, đề này có vẻ hơi độc à ha
Đúng 0
Bình luận (0)
Cho tam giác MNP có góc N là 50°, góc P là 70°, đường cao MK = 3,5cm. Sử dụng tỉ số lượng giác để tính các cạnh của tam giác MNP




