Tìm số nghiệm nguyên của phương trình 25 − x 2 ( l o g 2 ( x 2 − 4 x + 5 ) − 1 ) < 0
A. 6
B. 5
C. 4
D. 3
Tìm nghiệm nguyên của phương trình: \(x^2-25=y.\left(y+6\right)\)
x2 - 25 = y(y + 6)
<=> x2 - 25 = y2 + 6y
<=> x2 - 25 - y2 - 6y = 0
<=> \(\left\{{}\begin{matrix}x=\sqrt{6y+y^2+25}\\y=\sqrt{x^2-25-6y}\end{matrix}\right.\)
Tìm nghiệm nguyên của phương trình: \(x^2-25=y.\left(y+6\right)\)
tìm nghiệm nguyên của phương trình x^2-25=y(y+6)
\(x^2-25=y\left(y+6\right)\Leftrightarrow x^2-16=y^2+6y+9\Leftrightarrow x^2-\left(y+3\right)^2=16\)
\(\Leftrightarrow\left(x-y-3\right)\left(x+y+3\right)=16\)
Tới đây bạn tự làm nhé :)
sorry mk mới lớp 6 nên ko biết
2015(x^2 + y^2 ) - 2014(2xy+1) =25 . Tìm các nghiệm nguyên của phương trình
Tìm giá trị nguyên của n để nghiệm của phương trình sau là những số nguyên:
\(x^2-\left(n+4\right)x+\left(4n-25\right)=0\)
Tìm các nghiệm nguyên của phương trình sau: 7(x2+y2)=25(x+y)
Tìm số nghiệm nguyên của phương trình 25 - x 2 log 2 x 2 - 4 x + 5 < 0
A. 6
B. 5
C. 4
D. 3
Tìm số nghiệm nguyên của bất phương trình 25 - x 2 log 2 x 2 - 4 x + 5 ≤ 0
A. 6
B. 5
C. 4
D. 3
Đáp án D
Phương pháp:
- Tìm TXĐ
- Giải bất phương trình và tìm số nghiệm nguyên.
Cách giải:
Điều kiện xác định:
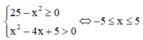
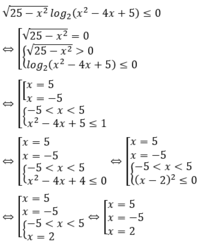
Vậy bất phương trình có 3 nghiệm nguyên.
Tìm các nghiệm nguyên của phương trình sau: 7(x2+y2) = 25(x+y)
tìm n thuộc Z để phương trình sau có nghiệm là số nguyên : x2 -(n+4)x+4n-25=0
\(\text{đen ta }=\left(n+4\right)^2-4\left(4n-25\right)=n^2+116\text{ là số chính phương}\)
đến đây thì là 1 bài đơn giản