Cho khai triển 3 + x 2019 = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ..... + a 2019 x 2019 . Hãy tính tổng S = a 0 − a 2 + a 4 − a 6 + ..... + a 2016 − a 2018
A. 3 1009
B. 0
C. 2 2019
D. 2 1009
PB
Những câu hỏi liên quan
MN
3 tháng 10 2020 lúc 20:49
Xét khai triển (1+x)(1+2x)(1+3x)....(1+2019x) = a0 + a1x + a2x2 + a3x3 +...+ a2019x2019. Tính S = 2a2 + (11 + 22 +...+ 20192)
\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)
cho đa thức F(x)= (2017x-2018)2019
khi khai triển ta đc đa thức bậc 2019
Tính tổng các hệ số của các số hạng của đa thức sau khi khai triển
đáp án =-1
Cho khai triển
(
1
+
2
x
)
2019
a
0
+
a
1
x
+
a
2
x
2
+
.
.
....
Đọc tiếp
Cho khai triển ( 1 + 2 x ) 2019 = a 0 + a 1 x + a 2 x 2 + . . . . . + a n x n . Tính tổng các hệ số trong khai triển?
A. 2019
B. 3 2019
C. 3 2020
D. 2 2019
Chọn B
Ta có 
Tổng các hệ số trong khai triển là: 
Cho x = 1 ta có: 
Đúng 0
Bình luận (0)
Cho biết 3 số hạng đầu của khai triển
x
+
1
2
x
n
,
x
0
có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên. A.
35
4
x...
Đọc tiếp
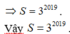
Cho biết 3 số hạng đầu của khai triển x + 1 2 x n , x > 0 có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên.
A. 35 4 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Cho biết 3 số hạng đầu của khai triển
x
+
1
2
x
n
,
x
0
có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên. A. ...
Đọc tiếp
Cho biết 3 số hạng đầu của khai triển x + 1 2 x n , x > 0 có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên.
A. 35 8 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Cho biết 3 số hạng đầu của khai triển
(
x
+
1
2
x
)
n
,
x
0
có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên A.
35
8...
Đọc tiếp
Cho biết 3 số hạng đầu của khai triển ( x + 1 2 x ) n , x > 0 có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên
A. 35 8 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Cho khai triển
x
+
2
x
6
với
x
0
. Tìm hệ số của số hạng chứa
x
3
trong khai triển trên. A. 80 B. 160 C. 240 D. 60
Đọc tiếp
Cho khai triển x + 2 x 6 với x > 0 . Tìm hệ số của số hạng chứa x 3 trong khai triển trên.
A. 80
B. 160
C. 240
D. 60
Đáp án là B
Ta có: x + 2 x 6 = ∑ k = 0 6 C 6 k 2 k x 6 − 3 2 k
Do đó số hạng chứa x 3 trong khai triển ứng với k thỏa mãn: 6 − 3 2 k = 3 ⇔ k = 2
Hệ số của x 3 trong khai triển là: C 6 2 2 2 = 60
Đúng 0
Bình luận (0)
Cho khai triển
x
+
2
x
6
với x0. Tìm hệ số của số hạng chứa
x
3
trong khai triển trên. A. 80 B. 160 C. 240 D. 60
Đọc tiếp
Cho khai triển x + 2 x 6 với x>0. Tìm hệ số của số hạng chứa x 3 trong khai triển trên.
A. 80
B. 160
C. 240
D. 60
(
x
+
2
)
n
+
5
,
(
n
∈
ℕ
)
Khai triển nhị thức có tất cả 2019 số hạng. Tìm n. A. 2018 B. 2014 C. 2013 D. 2015
Đọc tiếp
( x + 2 ) n + 5 , ( n ∈ ℕ ) Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
A. 2018
B. 2014
C. 2013
D. 2015
Chọn C
Khai triển ( x + 2 ) n + 5 , ( n ∈ ℕ ) có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013
Đúng 0
Bình luận (0)
Cho nhị thức
x
+
1
x
n
,
x
≠
0
trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng A. 252 B. 125 C. -252 D. 525
Đọc tiếp
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525
