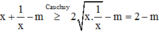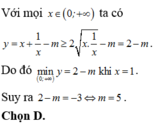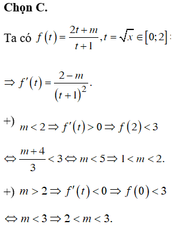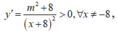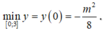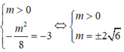Gọi m 0 là giá trị nhỏ nhất của tham số thực m để hàm số y = x 3 + 3 x 2 + m x + m nghịch biến trên một đoạn có độ dài bằng 1. Biết rằng m 0 = a b , a ∈ ℕ , b ∈ ℕ * và a b là phân số tối giản. Tính P = a b + a − b
A. P = 49
B. P = 41
C. P = 47
D. P = 36