Với số a bất kì, so sánh: a với a + 2
PB
Những câu hỏi liên quan
Với số a bất kì, so sánh: a với a – 1
Vì 0 > -1 nên 0 + a > a – 1. Suy ra: a > a – 1
Đúng 0
Bình luận (0)
cho m<n hãy so sánh
m+5, n+5
m-4,n-4
m-6,n+5
với số a bất kì hãy so sánh
a+1,a+4
a-2,3+a
a^2-a+3>a+2
a^2+a-1 với a>,= 1
Với số \(a\) bất kì, so sánh :
a) \(a\) với \(a-1\)
b) \(a\) với \(a+2\)
với a bất kì, ta luôn có:
a) a>a-1
b) a<a+2
Đúng 0
Bình luận (0)
a) 0 > -1 suy ra a > a - 1
b) 0 < 2 suy ra a < a + 2
Đúng 0
Bình luận (0)
Cho hình chữ nhật abcd. Trên cd lấy m bất kì, nối m với a và b. So sánh diện tích hình tam giác amb với tổng diện tích 2 hình tam giác adm và bmc ( không có số đo)
Cho 3 điểm A B C thẳng hàng , B nằm giữa A và C . Biết BA=2cm, BC=3cm. Lấy điểm H bất kì trên đường thẳng vuông góc với AC tại B
a) So sánh HB,HA và HC b) So sánh góc HAC và góc HCAc) So sánh góc BHA và góc BHCa: ΔHBA vuông tại B
=>HB<HA
Vì AB<BC
nên HA<HC
=>HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: HA<HC
=>góc HCA<góc HAC
=>góc AHB>góc BHC
Đúng 0
Bình luận (1)
bài 1:với 2 số nguyên a,b cùng dấu dương,so sánh a-1/a và b+1/b
bài 2:cho n là 1 số tự nhiên bất kì .cmr n+3 và 2n+5 là 2 số nguyên tố cùng nhau
bài 3:cho tổng S=1+3+5+...+2009+2011
CMR:n là 1 số chính phương
bài 4:cho A=2/3.4/5.6/7....4998/4999
Hãy so sánh A và 0,02
Cho AB = 6cm, C là điểm bất kì nằm giữa A và B.I là trung điểm AC, K là trung điểm BC.
a) Tính IK
b) So sánh AK với (AB + AC) :2
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
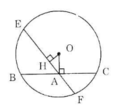
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
Đúng 0
Bình luận (0)
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
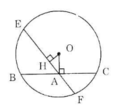
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
Đúng 0
Bình luận (0)



