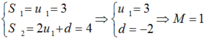Phát biểu định nghĩa cấp số cộng và công thức tính tổng n số hạng đầu tiên của một số không đổi d.
PB
Những câu hỏi liên quan
Phát biểu định nghĩa cấp số nhân và công thức tổng n số hạng đầu tiên của một cập số nhân.
+ Định nghĩa: Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó từ số hạng thứ hai; mỗi số hạng đều là tích các số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
(un) : un + 1 = un.q.
+ Tổng n số hạng đầu tiên của CSN.
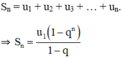
Đúng 0
Bình luận (0)
Cho cấp số cộng
u
n
có tổng của n số hạng đầu tiên được tính bởi công thức
S
n
4
n
–
n
^
2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó: A. M -1 B. M 1 C. M 4 D. M 7
Đọc tiếp
Cho cấp số cộng u n có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n – n ^ 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
A. M = -1
B. M = 1
C. M = 4
D. M = 7
Chọn B.
- Ta có: u 1 = S 1 = 3 .
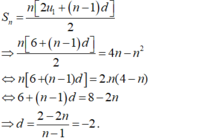
- Vậy M = u 1 + d = 3 - 2 = 1 .
Đúng 0
Bình luận (0)
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M=7
B. M=4
C. M= -1
D. M=1
Đáp án D
S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Đúng 0
Bình luận (0)
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = -1
D. M = 1
Đáp án D
Ta có: S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Đúng 0
Bình luận (0)
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n – n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = 2
D. M = 1
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
n
∈
N
*
. Tìm số hạng đầu
u
1
và công sai d của cấp số cộng đó. A. ...
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n n ∈ N * . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó.
A. u 1 = - 8 , d = 10
B. u 1 = - 8 , d = - 10
C. u 1 = 8 , d = 10
D. u 1 = 8 , d = - 10
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
,
(
n
∈
ℕ
*...
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ ℕ * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 ; d = 10 .
B. u 1 = - 8 ; d = - 10 .
C. u 1 = 8 ; d = 10 .
D. u 1 = 8 ; d = - 10 .
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
,
n
∈
ℕ
*
.
Tìm số hạng đầu
u
1
và công sai d của cấp số cộng đó. A....
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n , n ∈ ℕ * . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó.
A. u 1 = − 8 ; d = 10
B. u 1 = − 8 ; d = − 10
C. u 1 = 8 ; d = 10
D. u 1 = 8 ; d = − 10
Đáp án C
Ta có: S n = 2 u 1 + n − 1 d n 2 = d n 2 2 + u 1 − d 2 n = 5 n 2 + 3 n ⇒ d 2 = 5 u 1 − d 2 = 3 ⇔ d = 10 u 1 = 8 .
Đúng 0
Bình luận (0)
Một cấp số cộng có tổng n số hạng đầu
S
n
được tính theo công thức
S
n
5
n
2
+
3
n
,
(
n
∈
N
*
)
. Tìm số hạng đầu
u
1
và công sai d của cấp số cộng đó A.
u
1...
Đọc tiếp
Một cấp số cộng có tổng n số hạng đầu S n được tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ N * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 , d = 10
B. u 1 = - 8 , d = - 10
C. u 1 = 8 , d = 10
D. u 1 = 8 , d = - 10