cho tam giác MNP vuông tại P, PM=3cm,MN=6cm
CHo tam giác MNP vuông tại P, biết
a) PM = 6, MN = 10. Tính PN?
b) PM = 3, MN = 7. Tính PN?
c) Tam giác MNP vuông cân tại P có PM = 2. Tính PN, MN
Hình minh họa :)
a) Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> PN2 = MN2 - PM2
=> PN2 = 102 - 62
=> PN2 = 64
=> PN = 8
Vậy PN = 8
b) Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> PN2 = MN2 - PM2
=> PN2 = 72 - 32
=> PN2 = 40
=> PN = \(\sqrt{40}\)
Vậy PN = \(\sqrt{40}\)
c) Vì MNP cân tại P => PM = PN => PN = 2
Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> MN2 = 2 . 22
=> MN2 = 8
=> MN = \(\sqrt{8}\)
Vậy MN = \(\sqrt{8}\)
Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai
A. Tam giác ABC là tam giác vuông
B. Δ ABC và ΔMNP đồng dạng với nhau
C. NP = 10 cm
D. Có hai phương án sai
Ta có: A B 2 + A C 2 = B C 2 ( 3 2 + 4 2 = 5 2 = 25 )
Suy ra: tam giác ABC vuông tại A
Xét Δ ABC và Δ MNP có:
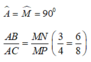
Suy ra: Δ ABC và ΔMNP đồng dạng với nhau.
Áp dụng định lí Pyta go vào tam giác MNP có:
N P 2 = M N 2 + M P 2 = 6 2 + 8 2 = 100 nên NP = 10cm
Chọn đáp án D
Cho tam giác ABC có AB = 3cm, AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; NP = 10cm . Tìm khẳng định sai?
A. Tam giác ABC là tam giác nhọn
B. Δ ABC đồng dạng tam giác MNP
C. Tam giác ABC vuông tại A.
D. MP = 8cm
cho tam giác abc vuông tại A có AB=3cm,BC=5cm và tam giác MNP vuông tại M có MN=6cm,NP=10cm.a,Chứng minh tam giác abc đồng dạng tam giác mnp.b,chỉ ra các cặp góc đồng dạng
a: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(MP=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xet ΔABC vuông tại A và ΔMNP vuông tại M co
AB/MN=AC/MP
=>ΔABC đồng dạng vơi ΔMNP
b: ΔABC đồng dạng vơi ΔMNP
=>goc A=góc M; góc B=góc N; gócC=góc P
Cho tam giác ABC có AB=3cm,BC=5cm,AC=6cm và tam giác MNP có MN=9cm,NP=4,5cm,PM=7,5cm.
CMR: tam giác ABC∼tam giác NPM
Giups mk vs ạ ai nhanh mk tick nha :>
Xét ΔABC và ΔNPM có
\(\dfrac{AB}{NP}=\dfrac{AC}{NM}=\dfrac{BC}{PM}\)
Do đó: ΔABC∼ΔNPM
7:Cho tam giác MNP vuông tại M ( ) MP MN . Kẻ tia phân giác của góc N cắt PM tại I. Từ P hạ đoạn thẳng PK vuông góc với tia phân giác NI ( K thuộc tia NI). a) Chứng minh MNI KPI ∽ ; b) Chứng minh INP IPK = ; c) Cho MN = 3cm, MP = 4cm. Tính IM.
Cho tam giác MNP vuông tại M,MN=6cm, góc P=30 độ Giải tam giác MNP
Cho tam giác MNP vuông tại M, có MN = 3cm, NP= 5cm. Giải tam giác vuông MNP ( góc làm tròn đến độ )
MP=4cm
\(\widehat{N}=53^0;\widehat{P}=37^0\)
Cho tam giác MNP vuông tại P . Phân giác góc M cắt NP tại A . Từ A kẻ AH vuông góc với MN a CHỨNG MINH PM bằng MH b MP cắt AH tại B CHỨNG MINH tam giác MNP bằng tam giác MBH
a: Xét ΔMPA vuông tại P và ΔMHA vuông tại H có
MA chung
\(\widehat{PMA}=\widehat{HMA}\)
Do đó: ΔMPA=ΔMHA
Suy ra: MP=MH
b: Xét ΔMNP vuông tại P và ΔMBH vuông tại H có
MP=MH
\(\widehat{PMN}\) chung
Do đó: ΔMNP=ΔMBH