Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác vuông cân tại đỉnh A, mặt bên B C C ' B ' là hình vuông, khoảng cách giữa A B ' v à C C ' bằng a. Thể tích của khối trụ A B C . A ' B ' C ' .
A. a 3
B. 2 a 3 2
C. 2 a 3 3
D. 2 a 3
Cho hình lăng trụ đứng ABC.A' B' C' có đáy là tam giác vuông cân đỉnh A, BC=2a, thể tích khối lăng trụ đã cho bằng a 3 . Khoảng cách từ điểm B' đến mặt phẳng (A' BC) bằng
A. 2 a B. 6 a 4 . C. 2 a 2 . D. 6 a 3
B. 6 a 4 .
C. 2 a 2 .
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy là tam giác vuông cân tại đỉnh A, mặt bên BCC’B’ là hình vuông, khoảng cách giữa AB’ và CC’ bằng a. Thể tích của khối trụ ABC. A’B’C’.
A. a 3
B. 2 a 3 2
C. 2 a 3 3
D. 2 a 3
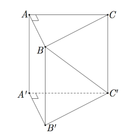
Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại A,AB=AA'=a (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BC′ và mặt phẳng (ACC′A′) bằng
A. 6 3
B. 2 2
C. 6 2
D. 3 3
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là các tam giác vuông cân tại A và A’, có BC = 3 2 cm và AB' = 5 cm. Tính:
a) Chiều cao của hình lăng trụ;
b) Diện tích của mặt bên ABB'A' và tổng diện tích của hai mặt đáy
Tương tự 3A.
a) Chiều cao lăng trụ là 4cm.
b) SABB'A'=12cm2 và S2đáy = 9cm2
Cho lăng trụ đứng ABC.A'B'C có đáy là tam giác vuông cân đỉnh A, mặt bên BCC’B' là hình vuông, khoảng cách giữa AB' và CC’ bằng a. Thế tích của khối trụ ABC.A'B'C?
A. 2 a 3 2
B. 2 a 3 3
C. 2 a 3
D. a 3
Đáp án A
Hướng dẫn giải:
Ta có C'C//(ABB'A')
![]()
Lại có C ' A ' ⊥ B B ' , C ' A ' ⊥ A ' B '
![]()
Khi đó B ' C ' = a 2
Mà BCC’B’ là hình vuông nên chiều cao của hình lăng trụ
Kết luận
V A B C . A ' B ' C ' = 1 2 a 2 . a 2 = a 2 3 2
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông cân tại A, mặt bên B C C ' B ' là hình vuông cạnh 2a. Thể tích của khối lăng trụ bằng
A. a 3
B. a 3 2
C. 2 a 3 3
D. 2 a 3
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A với BC = a và mặt bên AA’B’B là hình vuông. Thể tích khối lăng trụ ABC.A’B’C’ bằng
A. 2 8 a 3
B. 2 4 a 3
C. 1 4 a 3
D. 1 12 a 3
Một hình lăng trụ đứng ABC.A'B'C'(đáy là tam giác đều ABC) ở bên trong một hình trụ. Các đỉnh A, B, C, A', B', C' thuộc hình trụ. Hình lăng trụ đứng và hình trụ có cùng chiều cao. Cho biết chu vi tam giác ABC là 6cm, thể tích của hình lăng trụ đứng là 123 cm³. Hãy tính chiều cao và thể tích của hình trụ( kết quả làm tròn đến hàng đơn vị)
Chú ý: Thể tích hình trụ đứng = diện tích đáy nhân với chiều cao.
Diện tích tam giác đều là: AB^2√3/4
Thể tích hình trụ = diện tích đáy nhân với chiều cao.
AB=2cm
=>S ABC=căn 3(cm2)
=>h=12(cm)
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ
A. V = a 3
B. V = a 3 2
C. V = 2 a 3 3
D. V = 2 a 3