Tính tổng các hệ số trong khai triển ( 1 - 2 x ) 2019
A. -1
B. 2019
C. -2019
D. 1
Cho khai triển ( 1 + 2 x ) 2019 = a 0 + a 1 x + a 2 x 2 + . . . . . + a n x n . Tính tổng các hệ số trong khai triển?
A. 2019
B. 3 2019
C. 3 2020
D. 2 2019
Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
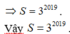
cho đa thức F(x)= (2017x-2018)2019
khi khai triển ta đc đa thức bậc 2019
Tính tổng các hệ số của các số hạng của đa thức sau khi khai triển
đáp án =-1
cho hàm số f(x)=ax2+bx+c ( x là ẩn , a,b,c là hệ số ) . Biết rằng f(0)=2018, f(1)=2019,f(-1)=2017 . Tính f(-2019)
cho đa thức f x = ax2 +bx + cx là biến số a b c là các hệ số biết f (0) = 2018; f(1) = 2019; f (-1) = 2017 .Tính f(-2019) ?
Ta có : f ( x ) = ax^2 + bx + c
Xét f ( 0 ) = a . 0^2 + b . 0 + c = 2018
=> c = 2018
Xét f ( 1 ) = a . 1^2 + b . 1 + c = 2019
=> a + b + c = 2019
= > a + b = 1 [ do c = 2018 theo trên rồi nhá ] ( 1 )
Xét f ( - 1 ) = a . ( -1 ) ^2 + b . ( -1 ) + c
=> a - b + c = 2017
=> a - b = -1 ( 2 )
Cộng ( 1 ) và ( 2 ) vế theo vế , ta được
a + b + a - b = 1 + ( - 1 )
= > 2. a = 0
= > a = 0
Trừ ( 1 ) và ( 2 ) vế theo vế ta được
a + b - a + b = 1 - ( - 1 )
=> 2 . b = 2
= > b = 1
Do đó : xét f ( - 2019 ) = a . ( - 2019 )^2 + b . ( - 2019 ) + c
=> 0 - 2019 + 2018
= - 1
Vậy f ( - 2019 ) = -1
[ nếu gặp các dạng bài này bạn cứ thay vào đa thức ban đầu rồi biến đổi tìm ra a , b , c nha ]
có thừa x ở cx ko ạ
cho đa thức f x = ax2 +bx + c là biến số a b c là các hệ số biết f (0) = 2018; f(1) = 2019; f (-1) = 2017 .Tính f(-2019) ?
Xét khai triển (1+x)(1+2x)(1+3x)....(1+2019x) = a0 + a1x + a2x2 + a3x3 +...+ a2019x2019. Tính S = 2a2 + (11 + 22 +...+ 20192)
\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)
Tìm x,y biết x^2018+y^2018=x^2019+y^2019=x^2020+y^2020.
Cho a+b+c=2019, 1/a + 1/b+1/c=1/2019. Tính 1/a^2019+1/b^2019+1/c^2019
Tìm x,y biết x^2-xy=6x-5y-8.
Giúp mk với, mk vã lắm rồi :-( :-(
gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> là sẽ tìm được nghiệm nguyên của
cho các số a,b,c khác 0 sao cho \(a+b=c+\frac{1}{2019}\)và \(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}+2019\)
tính giá trị của \(P=\left(a^{2019}+b^{2019}-c^{2019}\right)\left(\frac{1}{a^{2019}}+\frac{1}{b^{2019}}-\frac{1}{c^{2019}}\right)\)
\(a+b=c+\frac{1}{2019}\Leftrightarrow a+b-c=\frac{1}{2019}\Leftrightarrow\frac{1}{a+b-c}=2019\)
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}+2019\Rightarrow\frac{1}{a}+\frac{1}{b}-\frac{1}{c}=2019\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}-\frac{1}{c}=\frac{1}{a+b-c}\Rightarrow\frac{1}{a}+\frac{1}{b}=\frac{1}{a+b-c}+\frac{1}{c}\)
\(\Leftrightarrow\frac{a+b}{ab}=\frac{a+b}{c\left(a+b-c\right)}\Leftrightarrow c\left(a+b-c\right)\left(a+b\right)=\left(a+b\right)ab\)
\(\Leftrightarrow c\left(a+b-c\right)\left(a+b\right)-ab\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(ca+bc-c^2-ab\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left[c\left(a-c\right)-b\left(a-c\right)\right]=0\)
\(\Leftrightarrow\left(a+b\right)\left(c-b\right)\left(a-c\right)=0\)
=>a=-b hoặc c=b hoặc a=c
không mất tính tổng quát, giả sử a=-b, ta có:
\(P=\left(-b^{2019}+b^{2019}-c^{2019}\right)\left(-\frac{1}{b^{2019}}+\frac{1}{b^{2019}}-\frac{1}{c^{2019}}\right)=\left(-c\right)^{2019}\cdot\left(\frac{-1}{c}\right)^{2019}=1\)
tương tư với các trường hợp khác ta cũng có P=1
Vậy P=1
cho a+b=c+1/2019 ; 1/a+1/b=1/c+2019 tính A=(a^2019+b^2019-c^2019)(1/a^2019+1/b^2019-1/c^2019)
cho a+b=c+1/2019 ; 1/a+1/b=1/c+2019 tính A=(a^2019+b^2019-c^2019)(1/a^2019+1/b^2019-1/c^2019)
-(-219)+(-219)-401+12
https://olm.vn/hoi-dap/detail/108515110153.html