Tứ diện ABCD có AB=CD=4, AC=BD=5, AD=BC=6. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
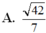
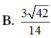
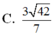
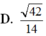
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tứ diện ABCD có A B = C D = 4 , A C = B D = 5 , A D = B C = 6. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 42 7
B. 3 42 14
C. 3 42 7
D. 42 14
Đáp án C
Phương pháp giải:
Áp dụng công thức tính nhanh thể tích của tứ diện gần đều, đưa bài toán tính khoảng cách về bài toán tìm thể tích chia cho diện tích đáy (tính theo công thức Hê – rông)
Lời giải:
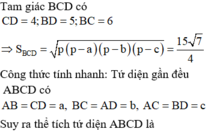
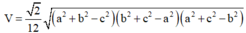

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Đáp án B
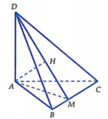
Ta có A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong (ABC) kẻ AM vuông góc tại M ⇒ 1 A M 2 = 1 A B 2 + 1 A C 2
Trong (DAM) kẻ A H ⊥ D M tại H.
Ta có
D A ⊥ B C ; A M ⊥ B C ⇒ D A M ⊥ B C ⇒ D A M ⊥ D B C
D A M ⊥ D B C D A M ∩ D B C = D M A H ⊂ D A M ; A H ⊥ D M ⇒ A H ⊥ D B C
⇒ d A ; D B C = A H
Tam giác DAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 A M 2 + 1 A D 2 = 1 A B 2 + 1 A C 2 + 1 A D 2 = 1 3 2 + 1 4 2 + 1 4 2 = 17 72 ⇒ A H = 12 34
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC=AD=4,AB=3, BC=5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
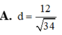
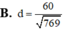
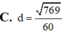
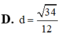
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC),AC =AD = 4, AB =3, BC = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Đáp án A
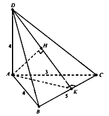
Vì B C 2 = B A 2 + A C 2 nên ∆ A B C vuông tại A.
Gọi K là hình chiếu của A lên BC, H là hình chiếu của A lên DK.
Ta có 1 A H 2 = 1 A D 2 + 1 A K 2 = 1 A D 2 + 1 A B 2 + 1 A C 2
= 1 4 2 + 1 4 2 + 1 3 2 = 17 72 ⇒ d A ; A B C D = A H = 72 17 = 12 34
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng A B C , A C = A D = 4 , A B = 3 , B C = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD)
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng ( A B C ) , A C = A D = 4 , B C = 5 . Tính khoảng cách d từ điểm A đến mặt phẳng (BCD)
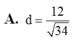
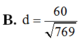
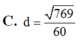
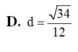
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3 cm, BC=4 cm, A D = 6 c m , AC=5 cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng
A. 12 5 cm
B. 12 7 cm
C. 6 cm
D. 6 10 cm
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o