Cho hai mặt cầu ( S 1 ) v à ( S 2 ) đồng tâm I, có bán kính lần lượt là R 1 = 2 v à R 2 = 10 . Xét tứ diện ABCD có hai đỉnh A , B nằm trên ( S 1 ) và hai đỉnh C , D nằm trên ( S 2 ) . Thể tích lớn nhất của khối tứ diện ABCD bằng
PB
Những câu hỏi liên quan
cho mặt cầu S và 2 mặt phẳng P và Q song song với nhau. biết rằng mặt phẳng P và Q lần lượt cắt mặt cầu S theo hai đường tròn có bán kính R1 và R2 và khoảng cách giữa mặt phẳng P và Q bằng a. tính bán kính của mặt cầu S theo R1; R2 và a
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
2
y
+
1
0
. Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)? A. 2 B. 0 C. 1 D. vô số
Đọc tiếp
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 y + 1 = 0 . Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)?
A. 2
B. 0
C. 1
D. vô số
Chọn C
Ta có: S : x - 1 2 + y - 1 2 + z 2 = 1 . Do đó (S) có tâm I(1;1;0) và bán kính R = 1.
Dễ kiểm tra A 1 ; 0 ; 0 ∈ S . Do đó mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A sẽ nhận 1 vectơ pháp tuyến là I A → 0 ; - 1 ; 0 . Phương trình của mặt phẳng P : y = 0 .
Do B ∈ P nên có duy nhất một mặt phẳng thỏa mãn là P : y = 0 .
Đúng 0
Bình luận (0)
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
2
+
1
0
. Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)?
Đọc tiếp
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 + 1 = 0 . Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)?
Trong không gian Oxyz, cho hai đường thẳng
△
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và △ 2 : x - 2 = y + 3 = z 1 Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng △ 1 và △ 2 Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
Trong không gian Oxyz, cho hai đường thẳng
∆
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2
và
∆...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng ∆ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và ∆ 2 : x - 2 1 = y + 3 3 = z 1 . Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng ∆ 1 và ∆ 2 . Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 0, (Q): 2x - y - 2z + 1 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu? A. 4π B. π C. 2π D. 16π
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
A. 4π
B. π
C. 2π
D. 16π
Đáp án A
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n → (2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
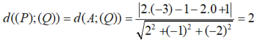
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu: 2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4π R 2 = 4 π
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
Δ
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2
và
Δ
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng Δ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và Δ 2 : x - 2 1 = y + 3 3 = z 1 . Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng Δ 1 v à Δ 2 . Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
Cho mặt cầu (S): x2 + (y-1)2 + (z-1)2 = 1 và đường thẳng d: x-2 = y = -z. Hai mặt phẳng (P) và (Q) chứa d, tiếp xúc với (S) tại P và Q. Tìm tọa độ trung điểm H của đoạn thẳng PQ
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
Đúng 0
Bình luận (0)
Cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
-
4
)
2
+
z
2
8
và hai điểm A(3;0;0), B(4;2;1). Gọi M là điểm thuộc mặt mặt cầu (S) Tính giá trị nhỏ nhất của biểu thức MA+2MB A. ...
Đọc tiếp
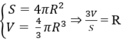
Cho mặt cầu (S): ( x + 1 ) 2 + ( y - 4 ) 2 + z 2 = 8 và hai điểm A(3;0;0), B(4;2;1). Gọi M là điểm thuộc mặt mặt cầu (S) Tính giá trị nhỏ nhất của biểu thức MA+2MB
A. 6
B. 2 6
C. 6 2
D. 3 2
