Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2
PB
Những câu hỏi liên quan
Cho tứ giác ABCD có số đo các cạnh là a,b,c,d (a,b,c,d là các số nguyên dương). Biết a,b,c,d đều là các ước của a+b+c+d. CMR: tứ giác ABCD có ít nhất hai cạnh bằng nhau.
Cho tứ giác ABCD với D=90 độ, A=60 độ, B=150 độ, CD=12cm. AB là cạnh hình vuông có diện tích là 108cm^2. Miền trg tứ giác có điểm M sao cho ABCM là hình bình hành. MH vuông DC
a) CM:MC là phân giác BCD
b) DMC là tam giác vuông tại M
c) Tam giác AMD cân
d) Tính AD,BC=>Tam giác ADB đều
Cho khối tứ diện đều ABCD cạnh bằng a. Gọi A', B', C', D' lần lượt là trọng tâm của tam giác BCD, ADC, DAB, ABC
a) Chứng minh A'B'C'D' cũng là khối tứ diện đều
b) Tính \(V_{A'B'C'D'}\) theo a
nên \(V_{A'B'C'D'}=\dfrac{1}{27}V_{ABCD}=\dfrac{\sqrt{2}}{324}a^2\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có độ dài các cạnh là a, b, c, d đều là các số tự nhiên. Biết tổng S = a + b + c + d chia hết cho a, cho b, cho c, cho d. Chứng minh rằng tồn tại hai cạnh của tứ giác bằng nhau.
Giả sử tứ giác ABCD có AD = a, AB = b, BC = c, CD = d không có hai cạnh nào bằng nhau. Ta có thể giả sử a < b < c < d.
Ta có a + b + c > BD + c > d.
Do đó a + b + c + d > 2d hay S > 2d (*)
Ta có: S\(⋮\)a => S = m.a (m\(\in\)N) (1)
S\(⋮\)b => S = n.b (n\(\in\)N) (2)
S\(⋮\)c => S = p.d (p\(\in\)N) (3)
S\(⋮\)d => S = q.d (q\(\in\)N) (4) . Từ (4) và (*) suy ra q.d > 2d => q > 2
Vì a < b < c < d (theo giả sử) nên từ (1), (2), (3) và (4) suy ra m > n > p > q > 2
Do đó q\(\ge\)3; p\(\ge\)4; n\(\ge\)5; m\(\ge\)6
Từ (1), (2), (3), (4) suy ra 1/m = a/S; 1/n = b/S; 1/p = c/S; 1/q = d/S
Ta có: \(\frac{1}{6}+\frac{1}{5}+\frac{1}{4}+\frac{1}{3}\ge\frac{1}{m}+\frac{1}{n}+\frac{1}{p}+\frac{1}{q}=\frac{a+b+c+d}{S}=1\)
hay \(\frac{19}{20}\ge1\)(vô lí)
Vậy tồn tại hai cạnh của tứ giác bằng nhau (đpcm)
Cho tam giác ABC đều , cạnh dài 2 cm , đường cao AH .
a) Vẽ D đối xứng vs A qua BC
b) Cm tứ giác ABCD là hình thoi
c) Tính diện tích tam giác ABC
d) Lấy điểm M trên cạnh BD ( M ko trùng B và D ) . Cm ddierm đối xứng của M qua H nằm giữa A và C .
Cho tứ diện ABCD có CDa
2
,
∆
ABC là tam giác đều cạnh a,
∆
ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
Đọc tiếp
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S). A.
R
a
5
B.
R
a
6
3
C.
R
a
6
5...
Đọc tiếp
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 5
B. R = a 6 3
C. R = a 6 5
C. R = a 3
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
Đọc tiếp
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S). A.
R
a
6
B.
R
a
6
3
C.
R
a
6
5...
Đọc tiếp
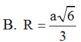
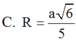
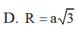
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 6
B. R = a 6 3
C. R = a 6 5
D. R = a 3
Đáp án là B
Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
Đúng 0
Bình luận (0)
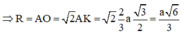
Cho S là diện tích của tứ giác ABCD có độ dài các cạnh là a, b, c, d. Chứng minh S ≤ (a^2 + b^2 + c^2 + d^2)/4