Phép biến đổi nào sau đây đúng với mọi a>0, mọi b>0
![]()
![]()
![]()
![]()
Với ∀ a > 0 , b > 0 . Chọn phép biến đổi đúng dưới đây
![]()
![]()
![]()
![]()
Bất đẳng thức nào sau đây đúng với mọi a > 0, b > 0?
A. a3 + b3 ≤ ab2 + a2b
B. a3 + b3 ≥ ab2 + a2b
C. ab2 + a2b = a3 + b3
D. ab2 + a2b > a3 + b3
Ta có: a3 + b3 - ab2 - a2b = a2(a - b) - b2(a - b)
= (a - b)2(a + b) ≥ 0 (vì (a - b)2 ≥ 0 với mọi a, b và a + b > 0 với a > 0, b > 0).
Do đó a3 + b3 - ab2 - a2b ≥ 0 hay a3 + b3 ≥ ab2 + a2b.
Đáp án cần chọn là: B
Bất đẳng thức nào sau đây đúng với mọi a > 0, b > 0?
A. a3 + b3 - ab2 - a2b < 0
B. a3 + b3 - ab2 - a2b ≥ 0
C. a3 + b3 - ab2 - a2b ≤ 0
D. a3 + b3 - ab2 - a2b > 0
Ta có a3 + b3 - ab2 - a2b = a2(a - b) - b2(a - b)
= (a - b)2(a + b) ≥ 0 (vì (a - b)2 ≥ 0 với mọi a, b và a + b > 0 với a > 0, b > 0).
Đáp án cần chọn là: B
Câu 28: Trong các nhận định sau, nhận định nào đúng?
A. mọi sự biến đổi về chất đều bắt nguồn từ sự biến đổi về lượng.
B. lượng và chất không có quan hệ gì với nhau.
C. mọi biến đổi về lượng đều dẫn đến sự biến đổi về chất.
D. mọi biến đổi về lượng đều dẫn đến sự ra đời của sự vật, hiện tượng mới.
Phép biến đổi nào sau đây đúng với ∀ x ∈ ℝ ?
![]()
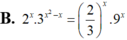
![]()
![]()
Bất đẳng thức nào sau đây không đúng với mọi x khác 0 và -1?
A. x + 1 2 ≥ 4 x
B. x + 1 2 x ≥ 4
C. x - 1 2 ≥ - 4 x
D. x x + 1 2 ≤ 1 4
Xét bất đẳng thức: x + 1 2 x ≥ 4
Với x = -3 thì - 3 + 1 2 - 3 ≥ 4 ( vô lí) .
Do đó, bất đẳng thức này không đúng với mọi x khác 0 và -1.
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án B
Đặt 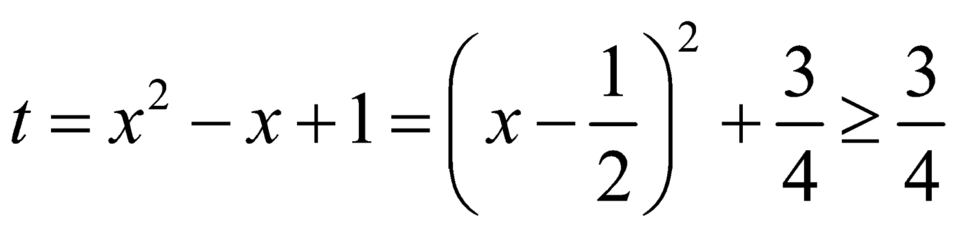
Ta có:
![]()
![]()
Đặt ![]() .
.
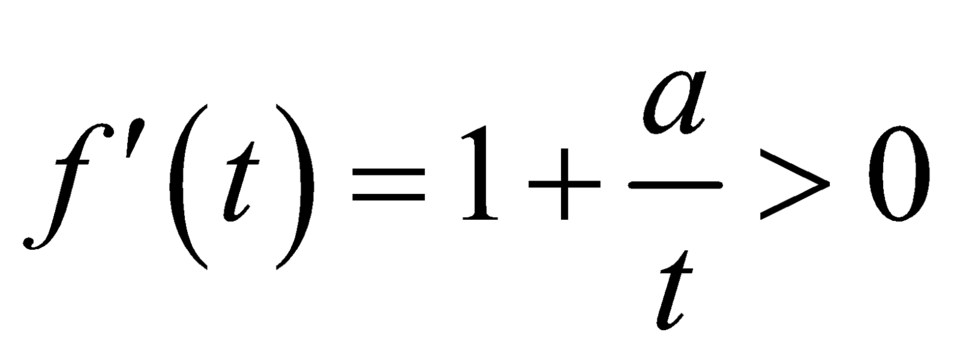
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 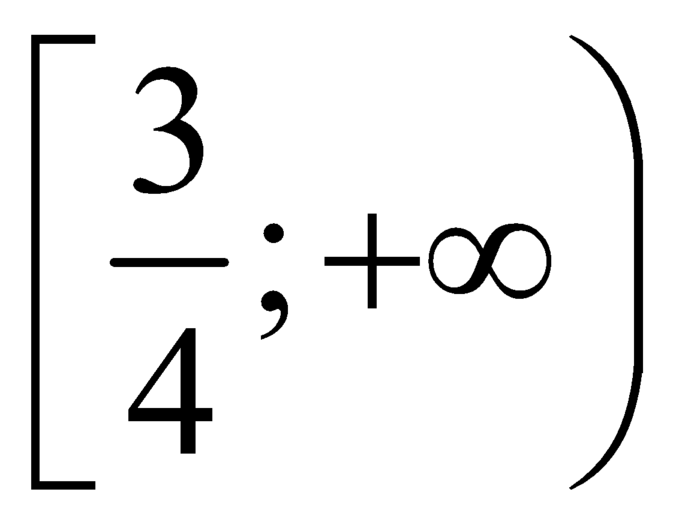 .
.
Khi đó 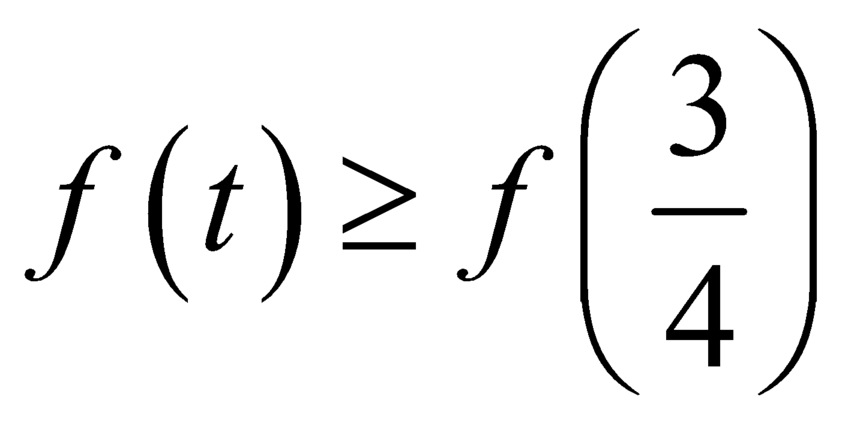
![]()
![]()
![]()
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Chọn đáp án C

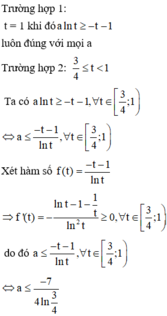
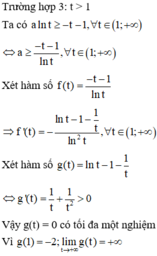
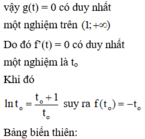
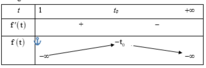

Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .