Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2].. Biết rằng F ( 0 )   =   0 ,   F ( 2 )   =   1 ,   G ( 0 )   =   - 2 ,   G ( 2 )   =   1 và ∫ 0 2 F x g x d x = 3 . Tích phân  ∫ 0 2 f x G x d x có giá trị bằng

A. 3

B. 0

C. -2

D. - 4

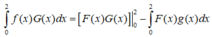
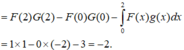
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và  ∫ 0 2 F ( x ) g ( x ) d x = 3  . Tính tích phân hàm:   ∫ 0 2 G ( x ) f ( x ) d x

A. I = 3.

B. I = 0.

C. I = -2.

D. I = -4.

 Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2]. Biết rằng F ( 1 )   =   1 ,   F ( 2 )   =   4 ,   G 1 = 3 2 ,   G 2 = 2   v à   ∫ 1 2 f x G x d x = 67 12 . Tích phân  ∫ 1 2 F x g x d x  có giá trị bằng

A.   11 12

B.  - 145 12

C.  - 11 12

D.  145 12

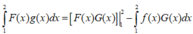
Cho f(x) là hàm số chẵn, liên tục trên R thỏa mãn ∫ 0 1 f ( x ) d x   =   2018  và g(x) là hàm số liên tục trên R thỏa mãn g ( x ) + g ( - x )   =   1  Tính tích phân  I   =   ∫ - 1 1 f ( x ) . g ( x ) d x

A. I = 2018

B. I = 504,5

C. I =4036

D. I = 1008

Cho f(x) là hàm số chẵn, liên tục trên ℝ  thỏa mãn ∫ 0 1 f x d x = 2018  và g(x) là hàm số liên tục trên ℝ  thỏa mãn g x + g − x = 1 , ∀ x ∈ ℝ .  Tính tích phân I = ∫ − 1 1 f x . g x d x  

A. I = 2018

B.  I = 1009 2

C. I = 4036

D. I = 1008

Cho f, g là hai hàm liên tục trên [1; 3] thỏa điều kiện  ∫ 1 3 f x + 3 g x d x = 10 đồng thời  ∫ 1 3 2 f x - g x d x = 6 . Tính  ∫ 1 3 f x + g x d x .

A. 8

B. 7

C. 9

D. 6

Cho f, g là hai hàm liên tục trên đoạn [1;3] thoả:  ∫ 1 3 f x + 3 g x d x = 10 ,   ∫ 1 3 2 f x - g x d x = 6 . Tính  ∫ 3 f x + g x d x .

A. 7.

B. 6.

C. 8.

D. 9

Cho f, g là hai hàm số liên tục trên [ 1 ; 3 ]  thỏa mãn:

∫ 1 3 f x + 3 g x d x = 10 ,      ∫ 1 3 2 f x − g x d x = 6.  Tính   ∫ 1 3 f x + g x d x

A. 9 

B. 8

C. 6

D. 7

Cho f, g là hai hàm liên tục trên [1;3] thỏa điều kiện ∫ 1 3 f x + 3 g x d x = 10  đồng thời ∫ 1 3 2 f x - g x d x = 6 . Tính  ∫ 1 3 f x + g x d x

A.  9.

B.  6.

C.  8.

D.  7.