Cho số thực m và hàm số y=f(x) có đồ thị như hình vẽ. Phương trình f ( 2 x + 2 - x ) = m nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?

A. 2
B. 3
C. 4
D. 5
Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
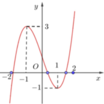
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình vẽ. Số nghiệm thực của phương trình f ( 2 + f ( e x ) ) = 1 là:
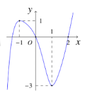
A. 1
B. 2
C. 4
D. 3
Cho số thực m và hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f 2 x + 2 - x có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?
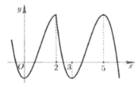
A. 2
B. 3
C. 4
D. 5
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=f(x) bằng
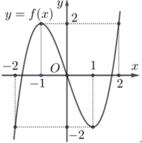
A. 7
B. 3
C. 6
D. 9
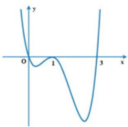
Cho hàm sốy=f(x) có đạo hàm f'(x) trên tập số thực ℝ và đồ thị của hàm số y=f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = ( f ( x ) ) 2 có
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
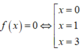
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
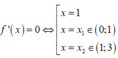
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
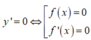
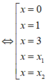
Ta có BXD của y' như sau
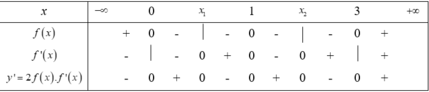
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x)) =0 bằng

A. 7
B. 3
C. 5
D. 9
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=0 bằng
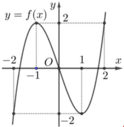
A. 7
B. 3
C. 5
D. 9

Vậy phương trình đã cho có tất cả 9 nghiệm.
Chọn đáp án D.
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ.
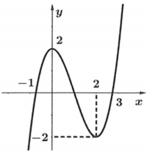
Gọi m là số nghiệm thực của phương trình f(f(x))=1 khẳng định nào sau đây là đúng ?
A.m=6
B.m=7
C.m=5
D. m=9
Đặt t =f(x) ta có f[f(x)]=1→f(t)=1
Dựa vào sự tương giao của đồ thị hàm số y=f(x) và đường thẳng y=1 ta thấy phương trình f(t)=1 có 3 nghiệm t =a ϵ (0 ;2),t =c ϵ(2 ;+∞) Dựa vào đồ thị ta lại có:
Phương trình t =a→f(x) =a và phương trình t =f(x) =b có 3 nghiệm phâ biệt.
Phương trình f =f(x) =c có một nghiệm duy nhất.
Vậy phương trình đã cho có 7 nghiệm .
Chọn đáp án B.