Cho hàm số có đồ thị (C). Gọi (d) là đường thẳng đi qua A (3;20) và có hệ số góc m. Giá trị của m để đường thẳng (d) cắt (C) tại 3 điểm phân biệt:
A. m < 15 4
B. m < 15 4 , m ≠ 24
C. m > 15 4 , m ≠ 24
D. m ≥ 15 4
Cho hàm số:y=x+m có đồ thị là đường thẳng (d)
a) Tìm m để đồ thị hàm số đi qua điểm D(1;-2) và vẽ đồ thị hàm số trong hệ trục
tọa độ Oxy. Cho biết điểm E(2;5) có thuộc đồ thị hàm số vừa vẽ không?
b) Gọi E và F lần lượt là giao điểm của đường thẳng (d) với hai trục Ox và Oy. Tìm
m để khoảng cách từ O đến đường thẳng EF bằng 3.
Giúp mik câu b vssss ;-;
\(a,\Leftrightarrow1+m=-2\Leftrightarrow m=-3\\ \Leftrightarrow y=x-3\\ \text{Thay }x=2;y=5\Leftrightarrow5=2-3=-1\left(\text{vô lí}\right)\\ \Leftrightarrow E\notinđths\\ b,\text{PT giao Ox và Oy: }\left\{{}\begin{matrix}y=0\Rightarrow x=-m\Rightarrow E\left(-m;0\right)\Rightarrow OE=\left|m\right|\\x=0\Rightarrow y=m\Rightarrow F\left(0;m\right)\Rightarrow OF=\left|m\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến EF
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}=\dfrac{1}{2m^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)
\(\Leftrightarrow m^2=\dfrac{9}{2}\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{\sqrt{2}}\\m=-\dfrac{3}{\sqrt{2}}\end{matrix}\right.\)
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Gọi (d) là đường thẳng đi qua A (3;20) và có hệ số góc m. Giá trị của m để đường thẳng (d) cắt (C) tại 3 điểm phân biệt:
![]()
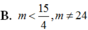
![]()
![]()
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C) . Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Giá trị của m để đường thẳng cắt (C) tại 3 điểm phân biệt là
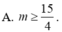
![]()
![]()
![]()
5. Tìm điều kiện của tham số để đồ thị hàm số đi qua một điểm A ( x0; y0) cho trước. y = (2 - m )x + m,Thì đồ thị hàm số đi qua A(-1; 6) 6. Tìm điều kiện của m để:Cho( d) :y = (m − 2)x + n (m ≠ 2). a) Đường thẳng (d) cắt đường thẳng (d1): −2y + x − 5 = 0 b) Đường thẳng (d) song song với đường thẳng(d2): 3x + y = 1 c) Đường thẳng (d) trùng với đường thẳng (d3): y = 2x + 3 7. Cho hàm số y = ( m+2)x + n-1 ( m -2) có đồ thị là đừờng thẳng (d) Cho n= 6,Gọi giao điểm của (d) với hai trục toạ độ là A, B.Tìm m để tam giác ABC có diện tích bằng 6
Cho hàm số bậc nhất y=(m+1)x-3 có đồ thị hàm số là đường thẳng d (m là tham số, m khác -1)
a) Tìm m để (d) đi qua E(4; 1) và vẽ đồ thị hàm số với m tìm được.
b) Cho (d’): y=5x-8 . Tìm m để (d) ⊥(d’).
c) Tìm m để đường thẳng (d) cắt đường thẳng y=3x-1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.
d) Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).
a: Thay x=4 và y=1 vào y=(m+1)x-3, ta được:
4(m+1)-3=1
=>4m+4-3=1
=>4m+1=1
hay m=0
b: Để hai đường vuông góc thì 5(m+1)=-1
=>m+1=-1/5
hay m=-6/5
c: Thay x=2 vào y=3x-1, ta được:
\(y=3\cdot2-1=5\)
Thay x=2 và y=5 vào (d), ta được:
2(m+1)-3=5
=>2(m+1)=8
=>m+1=4
hay m=3
Cho hàm số y = f(x) = (m+1)x – 2 có đồ thị là (d)
a. Tìm m biết rằng đồ thị (d) của hàm số đi qua A(-2:0)
b. Nêu tính chất và vẽ đồ thị hàm số với m tìm được ở câu a .
c. Không tính hãy so sánh f(2√3) và f(3√2)
d. Viết phương trình đường thẳng đi qua B(-1;1)và vuông góc với (d) nói trên
Câu 25: Chọn câu đúng nhất
A. Đồ thị hàm số ![]() là một đường thẳng
là một đường thẳng
B. Đồ thị hàm số![]() đi qua gốc tọa độ
đi qua gốc tọa độ
C. Đồ thị hàm số ![]() không đi qua gốc tọa độ
không đi qua gốc tọa độ
D. Đồ thị hàm số ![]() là một đường thẳng đi qua gốc tọa độ
là một đường thẳng đi qua gốc tọa độ
Câu 26: Phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn ?:
A. ![]() B.
B. ![]() . C.
. C. ![]() D.
D. ![]()
Câu 27: Nếu a ![]() b và b
b và b ![]() c thì :
c thì :
A. c // b B. a ![]() c C. a // c . D. a //b
c C. a // c . D. a //b
Câu 28: Trong các phân số sau, phân số biểu diễn số hữu tỉ ![]() là
là
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 29: Hai tia phân giác của hai góc đối dỉnh là :
A. Hai tia song song B. Hai tia vuông góc C. Hai tia đối nhau D. Hai tia trùng nhau
Câu 30: Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc bằng 900, thì:
A. xx’![]() yy’ B. xx’ là đường trung trực của yy’
yy’ B. xx’ là đường trung trực của yy’
C. xx’ // yy’ D. yy’ là đường trung trực của xx’
Câu 33: Kết quả của phép tính 325 : 35 là :
A. 120 B. 630 C. 320 D. 330
Câu 34: Qua điểm A ở ngoài đường thẳng a, có :
A. Một và chỉ một đường thẳng song song với a.
B. Vô số đường thẳng song song với a.
C. Hai đường thẳng song song với a.
D. Có ít nhất một đường thẳng song song với a.
Câu 35: Phát biểu nào sau đây đúng ?
A. Hai góc đối đỉnh luôn bằng nhau. B. Hai góc trong cùng phía luôn bù nhau
C. Hai góc so le trong luôn bằng nhau. D. Hai góc đồng vị luôn bằng nhau.
Câu 36: Kết quả phép tính ![]() bằng:
bằng:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 37: Nếu ![]() thì a2 bằng :
thì a2 bằng :
A. 3 B. 81 C. 27 D. 9
Câu 38: Câu nào sau đây đúng![]()
A. ![]() B.
B. ![]()
C. ![]() D. Cả ba câu trên đều sai
D. Cả ba câu trên đều sai
Câu 39: Kết quả của phép tính ![]() bằng
bằng
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 40: Cho ![]() và x –y = -22 khi đó giá trị cặp số x , y là :
và x –y = -22 khi đó giá trị cặp số x , y là :
A. x = 5; y =7 B. x = 55; y = 77 C. x = 55; y = -77 D. x = -55; y = 77
Câu 33: C
Câu 34: A
Câu 35: A
Cho hàm số bậc nhất y=(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y=2x+1 có đồ thị là đường thẳng (d')
a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)
b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d') .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
Câu 1: a) Cho hàm số y = ax + b, xác định a,b biết đồ thị hàm số đi qua điểm A( -1;2) và song song với đường thẳng y = 2x+3, vẽ đồ thị hàm số với giá trị a, b vừa tìm được b) Cho hàm số : y = mx – m + 2, có đồ thị là đường thẳng (d) Tìm tọa độ điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của m c) Tìm m để đường thẳng d cắt đường thẳng y = 2x -3 tại điểm nằm trên trục hoành. Câu 2: Cho đường tròn tâm O đường kính AB. Trên đường tròn lấy điểm C sao cho AC < BC (C khác A). Tiếp tuyến Bx của đường tròn (O) cắt đường trung trực của BC tại D. Gọi F là giao điểm của DO và BC. a) Chứng minh CD là tiếp tuyến của đường tròn (O) b) Gọi E là giao điểm của AD với đường tròn (O) (với E khác A). Chứng minh DE.DA = DC^2 = DF.DO c) Gọi H là hình chiếu của C trên AB, I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH.