Trong không gian cho tam giác OIM vuông tại I, I O M ^ = 30 ∘ , IM = a. Khi quay tam giác OIM quanh cạnh OI thì tạo thành một hình nón tròn xoay. Tính thể tích khối nón tròn xoay được tạo thành.
A. π a 3 3
B. π a 3 3
C. 2 π a 3 3
D. 2 π a 3 3
PB
Những câu hỏi liên quan
Trong không gian cho tam giác vuông OIM vuông tại I, góc OMI bằng 60 độ và cạnh IM bằng 2a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diện tích xung quanh là:
Trong không gian cho tam giác vuông OIM vuông tại I, góc OMI bằng 60 độ và cạnh IM bằng 2a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diện tích xung quanh là:
đường sinh l=2a:cos(60)=4a
S=πRl=2a.4aπ=8π\(a^2\)
Đúng 0
Bình luận (1)
Trong không gian cho tam giác OIM vuông tại I, góc
∠
I
O
M
45
0
và cạnh IM a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh
S
x
q
của hình nón tròn xoay đó theo a. A.
S
x
q...
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, góc ∠ I O M = 45 0 và cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh S x q của hình nón tròn xoay đó theo a.
A. S x q = π a 2 2
B. S x q = π a 2
C. S x q = π a 2 3
D. S x q = π a 2 2 2
Chọn A.
Phương pháp
Công thức tính diện tích xung quanh hình nón có bán kính đáy , R chiều cao h và đường sinh l: S x q = π R l .
Cách giải:
Đúng 0
Bình luận (0)
Trong không gian cho tam giác OIM vuông tại I, góc
I
O
M
^
45
°
và cạnh
I
M
a
. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh
S
x
q
của hình nón tròn xoay đó theo a
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, góc I O M ^ = 45 ° và cạnh I M = a . Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh S x q của hình nón tròn xoay đó theo a
Trong không gian cho tam giác OIM vuông tại I, góc
I
O
M
^
45
o
và cạnh IM a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh Sxq của hình nón tròn xoay đó theo a
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, góc I O M ^ = 45 o và cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh Sxq của hình nón tròn xoay đó theo a
Trong không gian cho tam giác OIM vuông tại I,
I
O
M
⏜
45
0
và cạnh IMa. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
Đọc tiếp
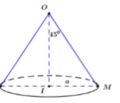
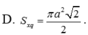
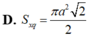
Trong không gian cho tam giác OIM vuông tại I, I O M ⏜ = 45 0 và cạnh IM=a. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
Trong không gian cho tam giác OIM vuông tại I,
I
O
M
45
°
và cạnh IM a Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng: A.
π
a
2
3
B.
π
a
2
C....
Đọc tiếp
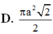
Trong không gian cho tam giác OIM vuông tại I, I O M = 45 ° và cạnh IM = a Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
A. π a 2 3
B. π a 2
C. π a 2 2
D. π a 2 2 2
Đáp án C
Phương pháp
+) Khi quay tam giác IOM quanh cạnh góc vuông OI ta được hình nón có đường cao IO và bán kính đáy IM.
+) Sử dụng công thức tính diện tích xung quanh của hình nón S x q = π r l trong đó r, l lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Cách giải
Khi quay tam giác IOM quanh cạnh góc vuông OI ta được hình nón có đường cao IO và bán kính đáy IM. Tam giác OIM vuông cân tại I nên IM = IO = a
⇒ r = a ; h = a ⇒ l = r 2 + h 2 = a 2 ⇒ S x q = π r l = π a . a 2 = π a 2 2
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho đường thẳng d: và điểm I(1;0;3).Tính khoảng cách từ điểm I đến đường thẳng d .Viết phương trình mặt cầu (S) có tâm I cắt d tại hai điểm A,B sao cho tam giác IAB vuông tại I
cho tam giác MNP cân tại M,gọi I là trung điểm NP
a) chứng minh tam giác MIN= tam giác MIP
b) Vẽ IA vuông góc MN tại A; IB vuông góc MP tại B.Chứng minh tam giác MAB cân tại M
c) Gọi O là trung điểm AB.Chứng minh 3 điểm M,O,I thẳng hàng