Cho hình chóp S.ABC có SA = SB = SC = a. ASB = 60 ∘ , BSC = 90 ∘ , CSA = 120 ∘ . Tính thể tích hình chóp S.ABC
A. 2 a 3 6
B. 2 a 3 12
C. 2 a 3 3
D. 2 a 3 4
PB
Những câu hỏi liên quan
Cho hình chóp S.ABC có SA 1, SB 2, SC 3 và
A
S
B
^
60
°
,
B
S
C
^
120
°
,
C
S
A
^
...
Đọc tiếp
Cho hình chóp S.ABC có SA = 1, SB = 2, SC = 3 và A S B ^ = 60 ° , B S C ^ = 120 ° , C S A ^ = 90 ° . Tính thể tích khối chóp S.ABC.
A. 2 2
B. 2
C. 2 6
Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM,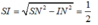 
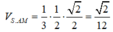
Ta có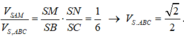 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có
S
A
S
B
S
C
a
,
A
S
B
^
60
°
,
B
S
C
^
90
°
,
C
S
A
^
120
°
. Khoảng cách từ đi...
Đọc tiếp
Cho hình chóp S.ABC có S A = S B = S C = a , A S B ^ = 60 ° , B S C ^ = 90 ° , C S A ^ = 120 ° . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A. a 3 2
B. a 3
C. a
D. a 2 2
Cho hình chóp S.ABC có ASB BSC CSA
60
°
,SA 2,SB 3. SC 6 Tính thể tích khối chóp S.ABC A.
6
2
(
đ
v
t
t
)
B.
18
2
(
đ
v
t
t
)
C.
9
2
(
đ
v
t
t
)
D.
3
2
(
đ
v...
Đọc tiếp
Cho hình chóp S.ABC có ASB = BSC = CSA = 60 ° ,SA = 2,SB = 3. SC = 6 Tính thể tích khối chóp S.ABC
A. 6 2 ( đ v t t )
B. 18 2 ( đ v t t )
C. 9 2 ( đ v t t )
D. 3 2 ( đ v t t )
Cho hình chóp tam giác S.ABC có
A
S
B
^
B
S
C
^
C
S
A
^
60
°
và
S
A
1
,
S
B
2
,
S...
Đọc tiếp
Cho hình chóp tam giác S.ABC có A S B ^ = B S C ^ = C S A ^ = 60 ° và S A = 1 , S B = 2 , S C = 3 . Thể tích của hình chóp S.ABC bằng
A. 2 6
B. 2 3
C. 2 2
D. 2 12
Cho hình chóp
S
.
A
B
C
D
có
A
S
B
B
S
C
C
S
A
60
°
,
S
A
2
,
S
B
3
,
S
C
6.
Tính thể tích khối chóp
S
.
A
B
C
A. ...
Đọc tiếp
Cho hình chóp S . A B C D có A S B = B S C = C S A = 60 ° , S A = 2 , S B = 3 , S C = 6. Tính thể tích khối chóp S . A B C
A. 6 2 d v t t
B. 18 2 d v t t
C. 9 2 d v t t
D. 3 2 d v t t
Đáp án D
Gọi B ' , C ' lần ượt là hai điểm thuộc SB, SC sao cho S B ' = S C ' = 2
Xét tứ diện S . A B ' C ' có A S B ' ⏜ = B ' S C ' ⏜ = C ' S A ⏜ = 60 ° S A = S B ' = S C ' = 2 ⇒ S . A B ' C ' là tứ diện đều cạnh 2
Khi đó V S . A B ' C ' = S A 3 2 12 = 2 3 2 12 = 2 2 3
mà V S . A B ' C ' V S . A B C = S B ' S B . S C ' S C = 2 3 . 2 6 = 2 9 .
Vậy V S . A B C = 3 2
Đúng 0
Bình luận (0)
Cho hình chóp
S
.
A
B
C
có
S
A
2
,
S
B
3
,
S
C
4.
Góc
A
S
B
^
45
∘
,
B
S
C...
Đọc tiếp
Cho hình chóp S . A B C có S A = 2 , S B = 3 , S C = 4. Góc A S B ^ = 45 ∘ , B S C ^ = 60 ∘ ,
C S A ^ = 90 ∘ . Tính khoảng cách từ điểm B đến mặt phẳng S A C .
A. 1 2
B. 3
C. 1
D. 3 2
Đáp án D
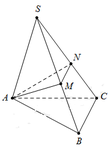
Gọi M, N lần lượt thuộc cạnh SB,SC sao cho S M = S N = 2.
Tam giác SMN đều ⇒ S M = S N = M N = 2.
Tam giác SAM có AS M ^ = 45 ∘ ⇒ A M = 2 2 − 2 .
Tam giác SAN vuông cân tại S ⇒ A N = S A 2 = 2 2 .
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ S I ⊥ A M N .
Tính bán kính đường tròn ngoại tiếp Δ A M N . Diện tích tam giác AMN là
S = p p − A M p − A N p − M N ⇒ R Δ A M N = A M . A N . M N 4 S = 2 4 − 2 2 S Δ A M N ,
với p = A M + A N + M N 2 .
Tam giác SAI vuông tại I, có S I = S A 2 − I A 2 = 4 − R 2 Δ A M N .
Ta có V S . A M N V S . A B C = S M S B . S N S C = 2 3 . 2 4 = 1 3 ⇒ V S . A B C = 3 V S . A M N ⇒ d B ; S A C = 9 V S . A M N S Δ S A C = 3 2 .
Đúng 0
Bình luận (0)
Cho khối chóp S.ABC có
A
S
B
^
B
S
C
^
C
S
A
^
60
°
,SAa,SB2a,SC4a. Tính thể tích khối chóp S.ABC theo a A.
8
a
3...
Đọc tiếp
Cho khối chóp S.ABC có A S B ^ = B S C ^ = C S A ^ = 60 ° ,SA=a,SB=2a,SC=4a. Tính thể tích khối chóp S.ABC theo a
A. 8 a 3 2 3
B. 2 a 3 2 3
C. 4 a 3 2 3
D. a 3 2 3
Cho hình chóp S.ABC có
SA
SB
SC
a
,
ASB
^
60
o
,
BSC
^
90
o
,
CSA
^
120
o
.
Tính thể tích hình chóp S.ABC. A.
2...
Đọc tiếp
Cho hình chóp S.ABC có SA = SB = SC = a , ASB ^ = 60 o , BSC ^ = 90 o , CSA ^ = 120 o . Tính thể tích hình chóp S.ABC.
A. 2 a 3 4
B. 2 a 3 12
C. 2 a 3 3
D. 2 a 3 6
Cho khối chóp S.ABC có SA 3, SB 4, SC 5,
A
S
B
^
B
S
C
^
C
S
A
^
60
°
. Thể tích khối chóp S.ABC bằng: A. ...
Đọc tiếp
Cho khối chóp S.ABC có SA = 3, SB = 4, SC = 5, A S B ^ = B S C ^ = C S A ^ = 60 ° . Thể tích khối chóp S.ABC bằng:
A. 5 2
B. 5 3
C. 10
D. 15
Chọn A.
Lấy N ∈ SB sao cho SN = 3/4.SB
Lấy M ∈ SC sao cho SM = 3/5.SC
Xét hình tứ diện đều SAMN cạnh x = 3 có 
Mặt khác 
Đúng 0
Bình luận (0)