Với số a bất kì, so sánh: a với a – 1
PB
Những câu hỏi liên quan
Với số a bất kì, so sánh: a với a + 2
Vì 0 < 2 nên 0 + a < a + 2. Suy ra: a < a + 2
Đúng 0
Bình luận (0)
cho m<n hãy so sánh
m+5, n+5
m-4,n-4
m-6,n+5
với số a bất kì hãy so sánh
a+1,a+4
a-2,3+a
a^2-a+3>a+2
a^2+a-1 với a>,= 1
Với số \(a\) bất kì, so sánh :
a) \(a\) với \(a-1\)
b) \(a\) với \(a+2\)
với a bất kì, ta luôn có:
a) a>a-1
b) a<a+2
Đúng 0
Bình luận (0)
a) 0 > -1 suy ra a > a - 1
b) 0 < 2 suy ra a < a + 2
Đúng 0
Bình luận (0)
bài 1:với 2 số nguyên a,b cùng dấu dương,so sánh a-1/a và b+1/b
bài 2:cho n là 1 số tự nhiên bất kì .cmr n+3 và 2n+5 là 2 số nguyên tố cùng nhau
bài 3:cho tổng S=1+3+5+...+2009+2011
CMR:n là 1 số chính phương
bài 4:cho A=2/3.4/5.6/7....4998/4999
Hãy so sánh A và 0,02
Cho 3 điểm A B C thẳng hàng , B nằm giữa A và C . Biết BA=2cm, BC=3cm. Lấy điểm H bất kì trên đường thẳng vuông góc với AC tại B
a) So sánh HB,HA và HC b) So sánh góc HAC và góc HCAc) So sánh góc BHA và góc BHCa: ΔHBA vuông tại B
=>HB<HA
Vì AB<BC
nên HA<HC
=>HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: HA<HC
=>góc HCA<góc HAC
=>góc AHB>góc BHC
Đúng 0
Bình luận (1)
Cho hình chữ nhật abcd. Trên cd lấy m bất kì, nối m với a và b. So sánh diện tích hình tam giác amb với tổng diện tích 2 hình tam giác adm và bmc ( không có số đo)
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
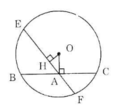
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
Đúng 0
Bình luận (0)
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
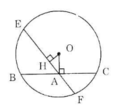
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
Đúng 0
Bình luận (0)
So sánh
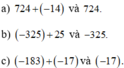
d) Em có nhận xét tổng của một số nguyên bất kì với một số nguyên âm (nguyên dương) với số đã cho?
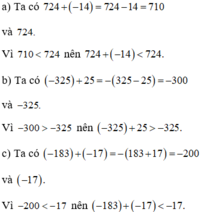
) Tổng của một số nguyên bất kì với một số nguyên âm luôn nhỏ hơn số đã cho. Tổng của một số nguyên bất kì với một số nguyên dương luôn lớn hơn số đã cho
Đúng 0
Bình luận (0)



