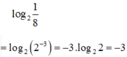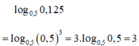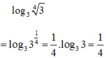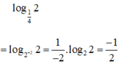Không sử dụng máy tính, hãy tính sin 40 0 - sin 45 0 + sin 50 0 cos 40 0 - cos 45 0 + cos 50 0 = 6 3 + 3 tan 15 ° 3 - 3 tan 15 °
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Không sử dụng bảng số và máy tính, hãy tính :
a) \(\sin^4\dfrac{\pi}{16}+\sin^4\dfrac{3\pi}{16}+\sin^4\dfrac{5\pi}{16}+\sin^4\dfrac{7\pi}{16}\)
b) \(\cot7,5^0+\tan67,5^0-\tan7,5^0-\cot67,5^0\)
a)\(sin^4\dfrac{\pi}{16}+sin^4\dfrac{3\pi}{16}+sin^4\dfrac{5\pi}{16}+sin^4\dfrac{7\pi}{16}\)
\(=\left(sin^4\dfrac{\pi}{16}+sin^4\dfrac{7\pi}{16}\right)+\left(sin^4\dfrac{3\pi}{16}+sin^4\dfrac{5\pi}{16}\right)\)
\(=\left(sin^4\dfrac{\pi}{16}+cos^4\dfrac{\pi}{16}\right)+\left(sin^4\dfrac{3\pi}{16}+cos^4\dfrac{3\pi}{16}\right)\)
\(=1-2sin^2\dfrac{\pi}{16}cos^2\dfrac{\pi}{16}+1-2sin^2\dfrac{3\pi}{16}cos^2\dfrac{3\pi}{16}\)
\(=2-\dfrac{1}{2}sin^2\dfrac{\pi}{8}-\dfrac{1}{2}sin^2\dfrac{3\pi}{8}\)
\(=2-\dfrac{1}{2}\left(sin^2\dfrac{\pi}{8}+sin^2\dfrac{3\pi}{8}\right)\)
\(=2-\dfrac{1}{2}\left(sin^2\dfrac{\pi}{8}+cos^2\dfrac{\pi}{8}\right)\)
\(=2-\dfrac{1}{2}=\dfrac{3}{2}\).
Đúng 0
Bình luận (0)
Có: \(cotx-tanx=\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}=\dfrac{cos^2x-sin^2x}{sinxcosx}=\dfrac{2cos2x}{sin2x}\)
Vì vậy:
\(cot7,5^o+tan67,5^o-tan7,5^o-cot67,5^o\)
\(=\left(cot7,5^o-tan7,5^o\right)-\left(cot67,5^o-tan67,5^o\right)\)
\(=\dfrac{2cos15^o}{sin15^o}-\dfrac{2cos135^o}{sin135^o}\)
\(=2\left(\dfrac{cos15^osin135^o-sin15^ocos135^o}{sin15^osin135^o}\right)\)
\(=2.\dfrac{sin120^o}{\dfrac{1}{2}\left(cos120^o-cos150^o\right)}\)
\(=\dfrac{4.\dfrac{\sqrt{3}}{2}}{\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}}=\dfrac{4\sqrt{3}}{\sqrt{3}-1}\)
Đúng 0
Bình luận (0)
* Tính ( không dùng máy tính)
\(\sin^235^0+tan22^0+sin^255^0-cotg13^0:tan77^0-cotg68^0\)
* Cho góc nhọn a, sina=\(\dfrac{2}{3}\)biết. Không tính số đo góc, hãy tính cosa, tân, cotga
Bài 2:
\(\cos\alpha=\sqrt{1-\dfrac{4}{9}}=\dfrac{\sqrt{5}}{3}\)
\(\tan\alpha=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\cot\alpha=\dfrac{\sqrt{5}}{2}\)
Đúng 1
Bình luận (0)
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
AB 6cm, b) AB 10cm, c) BC 20cm, d) BC 82cm, e) BC 32cm, AC 20cm f) AB 18cm, AC 21cm
Bài 4. Không sử dụng bảng số và máy tính, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: sin 650; cos 750; sin 700; cos 180; sin 790
Bài 5. Cho tam giác ABC cân ở A. Kẻ các đường cao AH và BK. Biết AB 10cm, BC 12cm.
a) Tính độ dài của đoạn thẳng AH, tính diện tích tam giác ABC.
b) Tính số đo góc ở đáy của tam giác cân ABC.
Đọc tiếp
AB = 6cm, b) AB = 10cm, c) BC = 20cm, d) BC = 82cm, e) BC = 32cm, AC = 20cm f) AB = 18cm, AC = 21cm Bài 4. Không sử dụng bảng số và máy tính, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: sin 650; cos 750; sin 700; cos 180; sin 790 Bài 5. Cho tam giác ABC cân ở A. Kẻ các đường cao AH và BK. Biết AB= 10cm, BC = 12cm. a) Tính độ dài của đoạn thẳng AH, tính diện tích tam giác ABC. b) Tính số đo góc ở đáy của tam giác cân ABC.
4:
\(cos75=sin15;cos18=sin72\)
\(15< 65< 70< 72\)
=>\(sin15< sin65< sin70< sin72\)
=>\(cos75< sin65< sin70< cos18\)
5:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=6cm
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2+6^2=10^2\)
=>HA2=64
=>HA=8(cm)
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot8\cdot12=4\cdot12=48\left(cm^2\right)\)
b: Xét ΔAHB vuông tại H có
\(sinB=\dfrac{AH}{AB}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq53^0\)
Đúng 1
Bình luận (0)
không sử dụng máy tính, hãy so sánh \(\sqrt{7}+\sqrt{11}+\sqrt{32}+\sqrt{40}\)và 18
\(\sqrt{7}+\sqrt{11}\)\(+\sqrt{32}+\sqrt{40}\) < 18
k mk nha
Đúng 0
Bình luận (0)
Không sử dụng máy tính, hãy tính: log 2 1 8
Không sử dụng máy tính, hãy tính: log 0 , 5 0 , 125
Không sử dụng máy tính, hãy tính: log 3 3 4
Không sử dụng máy tính, hãy tính: log 1 4 2
Không sử dụng máy tính, hãy tính :
a) \(\cos\dfrac{22\pi}{3}\)
b) \(\sin\dfrac{23\pi}{4}\)
c) \(\sin\dfrac{25\pi}{3}-\tan\dfrac{10\pi}{3}\)
d) \(\cos^2\dfrac{\pi}{8}-\sin^2\dfrac{\pi}{8}\)
a)
\(\cos\dfrac{22\pi}{3}=\cos\left(8\pi-\dfrac{2\pi}{3}\right)\\ =\cos\left(-\dfrac{2\pi}{3}\right)\\ =\cos\left(\dfrac{2\pi}{3}\right)\\ =-\cos\dfrac{\pi}{3}\\ =-\dfrac{1}{2}\)
b)
\(\sin\dfrac{23\pi}{4}=\sin\left(6\pi-\dfrac{\pi}{4}\right)\\ =\sin\left(-\dfrac{\pi}{4}\right)\\ =-\dfrac{\sqrt{2}}{2}\)
c)
\(\sin\dfrac{25\pi}{3}-\tan\dfrac{10\pi}{3}\\ =\sin\left(8\pi+\dfrac{\pi}{3}\right)-\tan\left(3\pi+\dfrac{\pi}{3}\right)\\ =\sin\dfrac{\pi}{3}-\tan\dfrac{\pi}{3}\\ =\dfrac{\sqrt{3}}{2}-\sqrt{3}\\ =\dfrac{-\sqrt{3}}{2}\)
d)
\(\cos^2\dfrac{\pi}{8}-\sin^2\dfrac{\pi}{8}\\ =\cos\dfrac{\pi}{4}\\ =\dfrac{\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
cau a: \(cos\dfrac{22\Pi}{3}=cos\dfrac{24\Pi-2\Pi}{3}=cos\left(8\Pi-\dfrac{2\Pi}{3}\right)=cos\dfrac{2\Pi}{3}=-\dfrac{1}{2}\)
câu b: \(sin\dfrac{23\Pi}{4}=sin\dfrac{24\Pi-\Pi}{4}=sin\left(6\Pi-\dfrac{\Pi}{4}\right)=-sin\dfrac{\Pi}{4}=-\dfrac{\sqrt{2}}{2}\)
cau c: \(=sin\left(8\Pi-\dfrac{\Pi}{3}\right)-tan\left(3\Pi+\dfrac{\Pi}{3}\right)=-sin\dfrac{\Pi}{3}-tan\dfrac{\Pi}{3}=-\dfrac{\sqrt{3}}{2}-\sqrt{3}=\dfrac{-3\sqrt{3}}{2}\)
cau d: \(cos^2\dfrac{\Pi}{8}-sin^2\dfrac{\Pi}{8}=cos2\left(\dfrac{\Pi}{8}\right)=cos\dfrac{\Pi}{4}=\dfrac{\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)