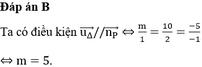Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 1 x
PB
Những câu hỏi liên quan
Cho ba hạt nhân X, Y và Z có số nuclôn tương ứng là
A
X
,
A
Y
,
A
Z
với
A
X
2
A
Y
0,5
A
Z
. Biết năng lượng liên kết của từng hạt nhân tương ứng là Δ
E
X...
Đọc tiếp
Cho ba hạt nhân X, Y và Z có số nuclôn tương ứng là A X , A Y , A Z với A X = 2 A Y = 0,5 A Z . Biết năng lượng liên kết của từng hạt nhân tương ứng là Δ E X , Δ E Y , Δ E Z với Δ E Z < Δ E X < Δ E Y . Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là
A. Y, X, Z
B. Y, Z, X
C. X, Y, Z
D. Z, X, Y
Đáp án A
Đặt
Đặt
Vậy tính bền vững của hạt nhân giảm dần theo thứu tự Y,X,Z
Đúng 0
Bình luận (0)
Cho hàm số có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y -x + 2 và tiếp xúc với (H) thì phương trình của Δ là A. y x + 4. D. Không tồn tại.
Đọc tiếp
Cho hàm số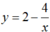 
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
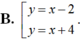
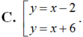
D. Không tồn tại.
Chọn C.
Đạo hàm: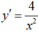 
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình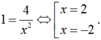 
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
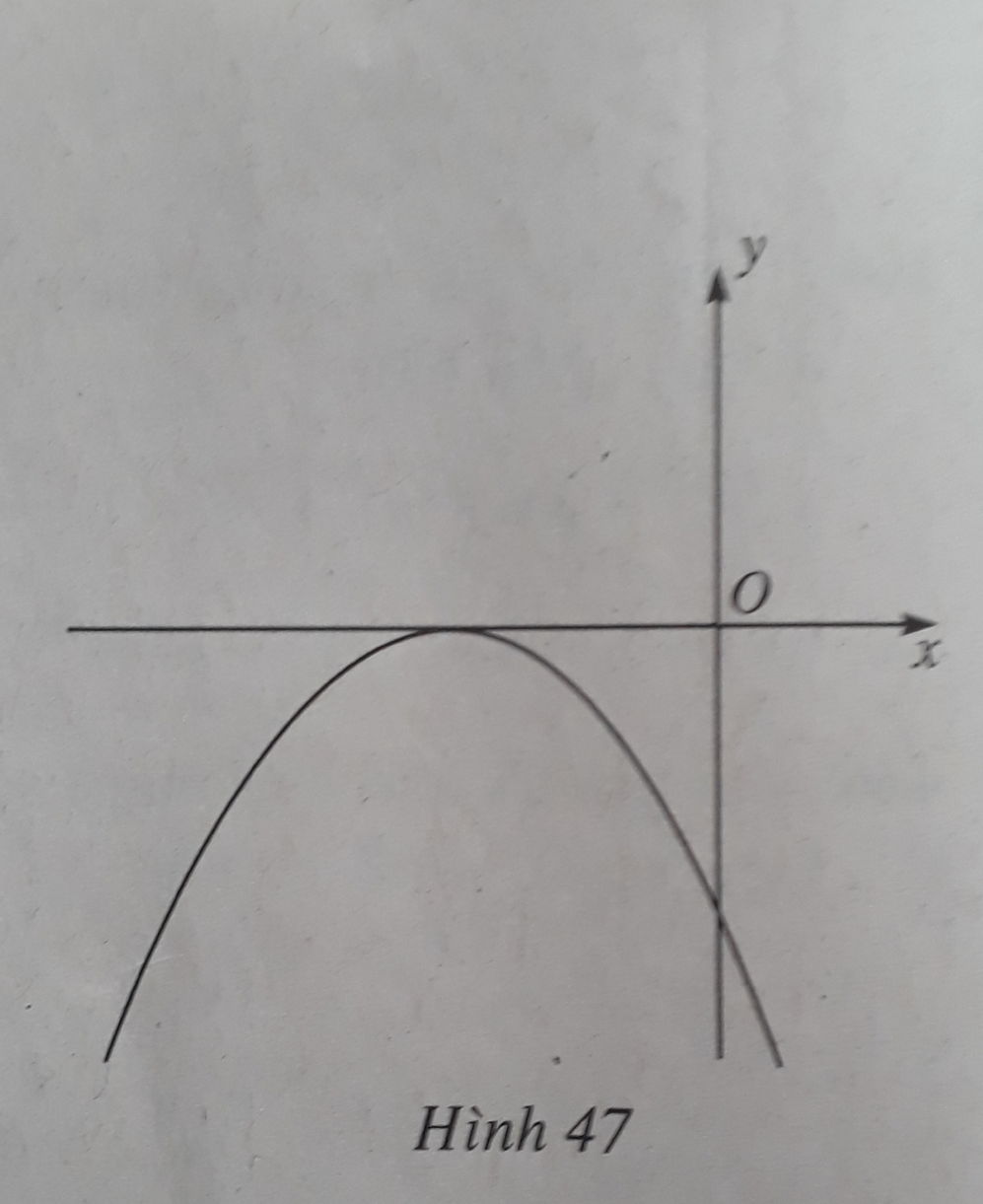
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Cho hàm số y=x2-2x-1 (P) , y=2x+1 (Δm)
a/ Tìm x để y>0, y<0, yminb/ Tìm giao điểm của (P) và đường thẳng :(Δ1): y=2x+1
mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Đồ thị (C) của hàm số cắt đường thẳng Δ: y -x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB A. I(-1;1). B. I(-2;2). C. I(3;-3). D. I(6;-6).
Đọc tiếp
Đồ thị (C) của hàm số cắt đường thẳng Δ: y = -x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB
A. I(-1;1).
B. I(-2;2).
C. I(3;-3).
D. I(6;-6).
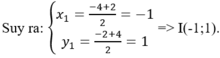
Đáp án A
Ta có: phương trình hoành độ giao điểm của (C) và 
(x ≠ 0).
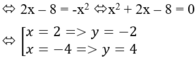
Gọi I(x1;y1) là trung điểm đoạn thẳng AB.
Đúng 0
Bình luận (0)
Hạt nhân
X
Z
1
A
1
bền hơn hạt nhân
Y
Z
2
A
2
, gọi Δ, Δ
m
2
lần lượt là độ hụt khối của X và Y. Biểu thức nào sau đây đúng? A.
A
1
Z...
Đọc tiếp
Hạt nhân X Z 1 A 1 bền hơn hạt nhân Y Z 2 A 2 , gọi Δ, Δ m 2 lần lượt là độ hụt khối của X và Y. Biểu thức nào sau đây đúng?
A. A 1 Z 1 > A 2 Z 2
B. Δ m 1 A 1 > Δ m 2 A 2
C. Δ m 1 A 2 > Δ m 2 A 1
D. A 1 Z 2 > A 2 Z 1
Chọn đáp án C
@ Lời giải:
+ Hạt nhân X bền hơn hạt nhân Y do vậy năng lượng liên kết riêng của nó lớn hơn Δ m 1 c 2 A 1 > Δ m 2 c 2 A 2
→ Δ m 1 A 2 > Δ m 2 A 1
Đúng 0
Bình luận (0)
Cho đường thẳng Δ có phương trình \(\left\{{}\begin{matrix}x=5t\\y=-1+6t\\z=2\end{matrix}\right.\) và mặt phẳng 2x-y-4z+3=0. Hình chiếu vuông góc d' của Δ lên mặt phẳng (P) theo phương d: \(\dfrac{x-1}{2}=\dfrac{y}{4}=\dfrac{z+3}{-1}\)
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
Δ
:
x
-
1
1
y
+
2
2
z
+
1
-
1
và mặt phẳng
(
α
)
:mx+10y-5z+10. Tìm tất cả các giá trị...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Δ : x - 1 1 = y + 2 2 = z + 1 - 1 và mặt phẳng ( α ) :mx+10y-5z+1=0. Tìm tất cả các giá trị của tham số m để Δ ⊥ ( α ) .
A. m=-25.
B. m=5.
C. m=25.
D. m=-5.
Cho Δ ABC có góc C = 30o. Gọi số đo các góc A, B lần lượt là x, y. Tính x và y trong mỗi trường hợp sau:
a) x = 2y
b) x - y = 10o
c*) 3x = 2y
Giải:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+30^o=180^o\)
\(\Rightarrow\widehat{A}+\widehat{B}=150^o\)
a) Ta có: \(\widehat{A}+\widehat{B}=150^o\)
\(\Rightarrow x+y=150^o\)
Mà x = 2y
\(\Rightarrow2y+y=150^o\)
\(\Rightarrow3y=150^o\)
\(\Rightarrow y=50^o\)
\(\Rightarrow x=50^o.2=100^o\)
Vậy \(y=50^o,x=100^o\)
b) Ta có: \(\widehat{A}+\widehat{B}=150^o\)
\(\Rightarrow x+y=150^o\)
Mà \(x-y=10^o\)
\(\Rightarrow x=\left(150^o+10^o\right):2=80^o\)
\(\Rightarrow y=150^o-80^o=70^o\)
Vậy \(x=80^o,y=70^o\)
c) Ta có: \(3x=2y\Rightarrow\frac{x}{3}=\frac{y}{2}\) và \(\widehat{A}+\widehat{B}=150^o\) hay \(x+y=150^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{150^o}{5}=30^o\)
+) \(\frac{x}{3}=30^o\Rightarrow x=90^o\)
+) \(\frac{y}{2}=30^o\Rightarrow y=60^o\)
Vậy \(x=90^o,y=60^o\)
Đúng 0
Bình luận (0)
Cho hai hàm số y2x2 có đồ thị (P) và yx+3 có đồ thị (d).a) Vẽ các đồ thị (P) và (d) trên cùng một mặt phẳng tọa Oxy.b) Gọi A là giao điểm của hai đồ thị (P) và (d) có hoành độ âm. Viết phương trình của đường thẳng (Δ) đi qua A và có hệ số góc bằng -1.c) Đường thẳng (Δ) cắt trục tung tại C, cắt trục hoành tại D. Đường thẳng (d) cắt trục hoành tại B. Tính tỉ số diện tích của hai Δ ABC và ΔABD.
Đọc tiếp
Cho hai hàm số y=2x2 có đồ thị (P) và y=x+3 có đồ thị (d).
a) Vẽ các đồ thị (P) và (d) trên cùng một mặt phẳng tọa Oxy.
b) Gọi A là giao điểm của hai đồ thị (P) và (d) có hoành độ âm. Viết phương trình của đường thẳng (Δ) đi qua A và có hệ số góc bằng -1.
c) Đường thẳng (Δ) cắt trục tung tại C, cắt trục hoành tại D. Đường thẳng (d) cắt trục hoành tại B. Tính tỉ số diện tích của hai Δ ABC và ΔABD.