Trong tam giác ABC có ∠ A = 30 o , ∠ B = 60 o . Trực tâm tam giác ABC là:
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm khác A, B, C
: Tam giác ABC có các góc A, B , C lần lượt tỉ lệ với các số 2; 3 và 4 thì số đo các góc của tam giác ABC là:
A. góc A bằng 40\(^o\); góc B bằng 60\(^o\) ; góc C bằng 80\(^o\)
B. góc A bằng 30\(^o\) ; góc B bằng 70\(^o\); góc C bằng 80\(^o\)
C. góc A bằng 80\(^o\); góc B bằng 60\(^o\); góc C bằng 40\(^o\)
A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*
Cho tam giác ABC = tam giác MNP. Biết góc B = 60o, góc P = 30o
a) CM tam giác ABC và tam giác MNP là các tam giác vuông
b) Vẽ MK vuông góc NP. Tính góc NMK và góc PNK
Bài làm
a) Vì tam giác ABC = tam giác MNP ( giả thiết )
=> \(\widehat{N}=\widehat{B}=60^0\)
\(\widehat{M}=\widehat{A}\)
\(\widehat{P}=\widehat{C}=30^o\)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( Định lý tổng ba góc của tam giác )
=> \(\widehat{A}=180^o-\widehat{B}-\widehat{C}\)
hay \(\widehat{A}=180^o-60^o-30^o\)
=> \(\widehat{A}=90^o\)
=> Tam giác ABC vuông tại A
Mà \(\widehat{A}=\widehat{M}\)( Chứng minh trên )
=> Tam giác MNP vuông tại M
b) Vì MK vuông góc với NP
=> tam giác MKN là tam giác vuông
=> \(\widehat{MAN}=90^o\)
Xét tam giác MKN vuông tại K
có: \(\widehat{N}+\widehat{NMK}=90^o\)( Hai góc phụ nhau )
hay \(60^o+\widehat{NMK}=90^o\)
=> \(\widehat{NMK}=90^o-60^o\)
=> \(\widehat{NMK}=30^o\)
Vậy \(\widehat{NMK}=30^o\)
Vì \(\widehat{NMP}=90^o\)( Chứng minh trên )
Ta có: \(\widehat{NMK}+\widehat{PKM}=\widehat{NMP}\)
hay \(30^o+\widehat{PKM}=90^o\)
=> \(\widehat{PKM}=90^o-60^o\)
=> \(\widehat{PKM}=30^o\)
Vậy \(\widehat{PKM}=30^o\)
~ Bạn ghi nhầm đề bài ak, nếu là tính góc PNK thì sai nha ~
# Chúc bạn học tốt #
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
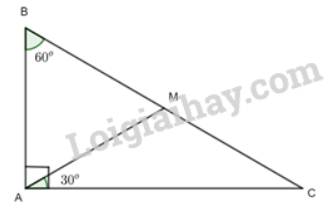
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
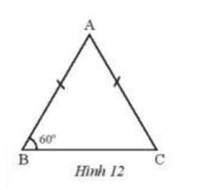
Ta có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều
a) Cho tam giác ABC vuông tại A. Tia phân giác BD chia AC thành 2 phần sao cho CD = 2AD. Tính số đo góc ABC.
b) Cho tam giác ABC có A = 70o, B = 60o. Đường tròn tâm O ngoại tiếp tam giác ABC. Tính số đo góc AOB.
a)
Theo tính chất đường phân giác áp dụng cho \(\Delta ABC\) có BD là phân giác góc ABC \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{1}{2}\)
\(\Delta ABC\) vuông tại A\(\Rightarrow\tan B=\frac{AB}{BC}=\frac{1}{2}\Rightarrow\widehat{B}\approx27\)
b,
Thấy \(\widehat{ACB}\) nội tiếp \(\left(O\right)\) chắn cung AB nhỏ
\(\Rightarrow\widehat{ACB}=\frac{1}{2}sđ\overline{AB}\left(1\right)\)
Thấy \(\widehat{AOB}\) chắn cung AB nhỏ \(\Rightarrow\widehat{AOB}=sđ\overline{AB}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AOB}=2\widehat{ACB}=2\left(180^o-70^o-60^o\right)=2.50^o=100^o\)
Cho tam giác ABC có góc A=60o, góc B=80o, tia phân giác trong của góc A cắt BC tại D. Tính số đo góc ADC.
GT : \(\widehat{BAC}=60^o\); \(\widehat{B}=80^o\); \(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{BAC}}{2}\)
KL : \(\widehat{ADC}=?\)
giải
vì AD là tia phân giác của \(\widehat{BAC}\)nên \(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{BAC}}{2}=\frac{60^o}{2}=30^o\)
Vì \(\widehat{ADC}\)là góc ngoài của \(\Delta BAD\)nên \(\widehat{ADC}=\widehat{BAD}+\widehat{ABD}\)
hay \(\widehat{ADC}=80^o+30^o=110^o\)
Vậy \(\widehat{ADC}=110^o\)
Cho tam giác ABC cân tại A , và góc A = 80o . Điểm M nằm trong góc A sao cho góc MAC = 60o , góc MCA = 30o . Tính góc MBC ?
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Bài 1: Cho tam giác ABC có \(\widehat{B}=60^o\), \(\widehat{C}=55^o\), AC = 4,5cm. Tính diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)
Cho tam giác ABC cân đỉnh B có góc B = 80o lấy điểm I trong tam giác ABC sao cho góc BAI = 10o , góc ICA = 30o Tính góc AIB