Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 5 n − 1 , n = 1 , 2 , 3 ... Tìm số hạng đầu u 1 và công bội q của cấp số nhân đó.
A. u 1 = 5 , q = 6
B. u 1 = 4 , q = 5
C. u 1 = 5 , q = 4
D. u 1 = 6 , q = 5
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là:
A. 1 S .
B. 1 q n . S .
C. S q n − 1 .
D. q n S .
Đáp án C
Em có: S = 1. q n − 1 q − 1 = q n − 1 q − 1 .
Vì cấp số nhân mới tạo thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu thành nghịch đảo của nó nên cấp số nhân mới sẽ có công bội là 1 q .
Gọi S' là tổng mới của cấp số nhân mới.
Em có: S ' = 1 q n − 1 1 q − 1 = 1 − q n q n . 1 − q q = 1 − q n 1 − q . 1 q n − 1 = S q n − 1 .
Vậy tổng của cấp số nhân mới là: S q n − 1 .
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho
A. 120005
B. 6840
C. 7775
D. 6480
Chọn D
Cấp số nhân u n có số hạng đầu u 1 và công bội q
Do S n = 6 n - 1 nên q ≠ 1
Khi đó S n = u 1 ( 1 - q n ) 1 - q = 6 n - 1
Ta có : S 1 = u 1 ( 1 - q ) 1 - q ⇔ u 1 = 5
S 2 = u 1 1 - q 2 1 - q ⇔ q = 6
Vậy u 5 = u 1 . q 4 = 6480
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho.
A. 120005
B. 6840
C. 7775
D. 6480
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số nhân ( u n ) có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số cộng đã cho
A. 6480
B. 6840
C. 7775
D. 12005
Chọn đáp án A
Phương pháp
u 5 = S 5 - S 4
Cách giải
Ta có:
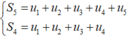
![]()
Cho cấp số nhân ( u n ) có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số cộng đã cho
A. 6480
B. 6840
C. 7775
D. 12005
Bài toán yêu cầu bạn tính tổng của một cấp số nhân có công bội là 3 và số hạng đầu tiên là 3. Công thức tính tổng của một cấp số nhân là:
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
Trong đó, $a_1$ là số hạng đầu tiên, $q$ là công bội, và $n$ là số hạng. Áp dụng công thức này vào bài toán của bạn, ta có:
$$A = 3^1 + 3^2 + 3^3 + ....... + 3^50 = \frac{3(1-3^{50})}{1-3}$$
Để tính giá trị của A, bạn có thể sử dụng máy tính hoặc các trang web chuyên về toán học. Mình đã tìm thấy một trang web có thể giải quyết bài toán này cho bạn. Theo trang web đó, kết quả của A là:
$$A \approx 7.178979876e23$$
Đây là một số rất lớn, gần bằng 718 nghìn tỷ tỷ tỷ. Hy vọng bạn đã hiểu cách giải bài toán này. Nếu bạn có thắc mắc gì khác, xin vui lòng liên hệ với mình. Mình rất vui khi được giúp đỡ bạn
cho cấp số nhân (Un) có tổng n số hạng đầu tiên là Sn = 4n-2n tìm công bội q của cấp số nhân đó
\(S_1=u_1=4-2=2\)
\(S_2=u_1+u_2=4^2-2.2=12\Rightarrow u_2=12-2=10\)
\(\Rightarrow q=\dfrac{u_2}{u_1}=\dfrac{10}{2}=5\)
Cho cấp số cộng (un) có công thức tổng quát là un =5-2n, n ∈ N * Tính tổng 20 số hạng đầu tiên của cấp số cộng.
A. -350
B. 440
C. -320
D. -340