Số nghiệm thuộc khoảng 0 ; 3 π của phương trình cos 2 x + 5 2 cos x + 1 = 0 là
A. 2
B. 4
C. 3
D. 1
Tìm số nghiệm thuộc khoảng 0 ; π của phương trình cos x + π 4 = 0
A. 0.
B. 1.
C. 2.
D. 3.
Tìm số nghiệm thuộc khoảng ( 0 ; π ) của phương trình cos ( x + π 4 ) = 0.
A. 0
B. 1
C. 2
D. 3
Tìm số nghiệm thuộc khoảng 0 , π của phương trình cos x + π 4 = 0
A. 0
B. 1
C. 2
D. 3
Tìm số nghiệm của phương trình cos22x + 3cos18x + 3cos14x + cos10x = 0 thuộc khoảng 0 ; π 2
A. 6
B. 7
C. 8
D. 9
Số nghiệm thuộc nửa khoảng - π ; 0 của phương trình cos x - cos 2 x - cos 3 x = 0 là
![]()
![]()
![]()
![]()
Số nghiệm thuộc nửa khoảng [ - π ; 0 ) của phương trình cosx-cos2x-cos3x+1 = 0 là
A. 3.
B. 1.
C. 4.
D. 2.
Chọn D
Phương trình tương với:
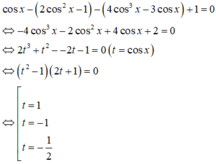
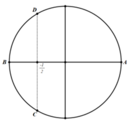
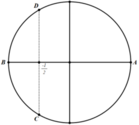
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π và - 2 π 3 ).
Số nghiệm thuộc nửa khoảng [ − π ; 0 ) của phương trình cos x − cos 2 x − cos 3 x + 1 = 0 là
A. 3
B. 1
C. 4
D. 2
Đáp án D.
Phương trình tương với:
cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π và − 2 π 3 ).
\(\dfrac{cos4x}{cos2x}=tan2x\)
có số nghiệm thuộc khoảng (0;\(\left(0;\dfrac{\pi}{2}\right)\)
\(\dfrac{cos4x}{cos2x}=tan2x\). ĐKXĐ : \(x\ne\dfrac{\pi}{4}+k.\dfrac{\pi}{2}\), k là số nguyên (tức là sin2x khác 1 và -1)
⇒ cos4x = sin2x
⇔ 1 - 2sin22x = sin2x
⇔ 2sin22x + sin2x - 1 = 0
⇔ \(\left[{}\begin{matrix}sin2x=-1\left(/\right)\\sin2x=\dfrac{1}{2}\left(V\right)\end{matrix}\right.\)
Mà x ∈ \(\left(0;\dfrac{\pi}{2}\right)\)
⇒ \(\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
cos 4 x cos 2 x = tan 2 x có số nghiệm thuộc khoảng 0 ; π 2 là:
A. 1
B. 3
C. 4
D. 2
Đáp án D
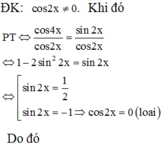
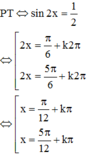
Do đó PT có 2 nghiệm thuộc khoảng 0 ; π 2