Cho ba số tự nhiên A; B và C có tổng là 5850, trong đó số A bé hơn số B là 15 đơn vị, số B bé hơn số C là 30 đơn vị. Tìm số C. Trả lời: Số C là
DA
Những câu hỏi liên quan
Cho 3 số tự nhiên 7,11 và a. Biết số tự nhiên a bằng trung bình cộng của ba số tự nhiên đã cho. tìm số tự nhiên a.
Xem chi tiết
a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9
Đúng 1
Bình luận (0)
Cho ba số tự nhiên 7,11 và a. Biết số tự nhiên a bằng trung bình cộng của 3 số tự nhiên đã cho. Tìm số tự nhiên a.
Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
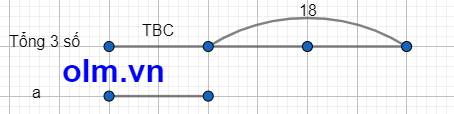
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9
Đúng 2
Bình luận (0)
Cho hai số tự nhiên 99;100. Hãy tìm số tự nhiên a để ba số có được tạo thành ba số tự nhiên liên tiếp A. 98 B. 97 C. 101 D. Cả A, C đều đúng
Đọc tiếp
Cho hai số tự nhiên 99;100. Hãy tìm số tự nhiên a để ba số có được tạo thành ba số tự nhiên liên tiếp
A. 98
B. 97
C. 101
D. Cả A, C đều đúng
Đáp án cần chọn là: D
Số liền trước số 99 là 98 nên ba số tự nhiên liên tiếp là 98;99;100
Số liền sau số 100là 101 nên ba số tự nhiên liên tiếp là 99;100;101
Vậy cả hai số 98;101đều thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án là D
liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Đúng 0
Bình luận (0)
Cho hai số tự nhiên 88;89. Hãy tìm số tự nhiên a để ba số có được tạo thành ba số tự nhiên liên tiếp.
A. 87
B. 90
C. 91
D. Cả A, B đều đúng
Đáp án cần chọn là: D
Số liền trước số 88 là số 87 nên ba số tự nhiên liên tiếp là 87;88;89
Số liền sau số 89 là số 90 nên ba số tự nhiên liên tiếp là 88;89;90
Vậy cả hai số 87;90đều thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp? A. 98 B. 97 C. 101 D. Cả A và C
Đọc tiếp
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án là D
Số liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Đúng 0
Bình luận (0)
Câu 9:
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B .97
C. 101
D. Cả A và C
Câu 9:
Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B .97
C. 101
D. Cả A và C
✔✔
Đúng 2
Bình luận (1)
Tìm bội chung nhỏ nhất của ba số: Số tự nhiên bé nhất có hai chữ số chia hết cho 2, số tự nhiên bé nhất có ba chữ số chia hết cho 5 và số tự nhiên bé nhất có ba chữ số chia hết cho 7.
A. 1680
B. 2100
C. 2500
D. 1260
chứng tỏ rằng :
a) tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3
b) tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4
c) tích của hai số tự nhiên liên tiếp thì chia hết cho 2
d) tích của ba số tự nhiên liên tiếp luôn chia hết cho 3
cứu mình
a, Gọi 3 số tự nhiên liên tiếp là n; n+1 và n+2
Tổng chúng: n+(n+1)+(n+2)= 3n+3\(⋮\) 3 \(\forall n\in N\) (đpcm)
b, Gọi 4 số tự nhiên liên tiếp là n; n+1; n+2; n+3
Tổng chúng: \(n+\left(n+1\right)+\left(n+2\right)+\left(n+3\right)=4n+6⋮̸4\forall n\in N\left(Vì:4n⋮4;6⋮̸4\right)\left(đpcm\right)\)
Đúng 2
Bình luận (0)
c, Hai số tự nhiên liên tiếp là k và k+1
Tích chúng: k(k+1) . Nếu k chẵn thì k+1 lẻ => Tích chẵn, chia hết cho 2
Nếu k lẻ thì k+1 chẵn => Tích chẵn, chia hết cho 2
(ĐPCM)
d, Ba số tự nhiên liên tiếp là m;m+1 và m+2
Tích chúng: m(m+1)(m+2)
+) TH1: Nếu m chia hết cho 3 => Tích 3 số chia hết cho 3
+) TH2: Nếu m chia 3 dư 1 => m+2 chia hết cho 3 => Tích 3 số chia hết cho 3
+) TH3: Nếu m chia 3 dư 2 => m+1 chia hết cho 3 => Tích 3 số chia hết cho 3
=> Kết luận: Tích 3 số tự nhiên liên tiếp chia hết cho 3 (đpcm)
Đúng 2
Bình luận (1)
a: Gọi ba số liên tiếp là a;a+1;a+2
a+a+1+a+2=3a+3=3(a+1) chia hết cho 3
b: Gọi 4 số liên tiếp là a;a+1;a+2;a+3
a+a+1+a+2+a+3
=4a+6
=4a+4+2
=4(a+1)+2 ko chia hết cho 4
c: Hai số liên tiếp thì luôn có 1 số chẵn, 1 số lẻ
=>Hai số liên tiếp khi nhân với nhau sẽ chia hết cho 2
d: Ba số liên tiếp thì chắc chắn sẽ có 1 số chia hết cho 3
=>Ba số liên tiếp khi nhân với nhau sẽ chia hết cho 3
Đúng 1
Bình luận (2)
Chứng tỏ rằng :
a) Trong hai số tự nhiên liên tiếp có một số chia hết cho 2
b) Trong ba số tự nhiên liên tiếp có một số chia hết cho 3
c) Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4
d) Tổng của ba số tự nhiên lien tiếp là một số chia hết cho ba
a; hai số tự nhiên liên tiếp có dạng: n; n + 1
Nếu n \(⋮\) 2 vậy trong hai số tự nhiên liên tiếp có một số chia hết cho 2
Nếu n = 2k + 1 thì n + 1 = 2k + 1 + 1 = 2k + (1 + 1) = 2k + 2 ⋮ 2
Từ những lập luận trên ta có hai số tự nhiên liên tiếp luôn có một số chia hết cho hai
Đúng 0
Bình luận (0)
b; Ba số tự nhiên liên tiếp có dạng: n; n + 1; n + 2
Nếu n ⋮ 3 thì trong ba số tự nhiên liên tiếp luôn có một số chia hết cho 3
Nếu n : 3 dư 1 hoặc 2 thì n có dạng: m = 3k + 1 hoặc n = 3k + 2
Trường hợp n = 3k + 1
khi đó n + 2 = 3k + 1 + 2 = 3k + (1 + 2) = 3k + 3 ⋮ 3
Trường hợp n = 3k + 2 thì n + 1 = 3k + 1 + 2 = 3k + (2 + 1) = 3k + 3
Từ những lập luận trên ta có:
Trong ba số tự nhiên liên tiếp luôn có một số chia hết cho 3
Đúng 0
Bình luận (0)
c; Bốn số tự nhiên liên tiếp có dạng:
n; n + 1; n + 2; n + 3
Khi đó tổng của bốn số tự nhiên liên tiếp là:
n + n + 1 + n + 2 + n + 3
= (n + n + n + n) + (1+ 2 + 3)
= 4n + (3+ 3)
= 4n + 6
= 4(n + 1) + 2 mà 2 không chia hết cho 4
Vậy tổng của bốn số tự nhiên liên tiếp không chia hết cho 4
Đúng 0
Bình luận (0)
Xem thêm câu trả lời





