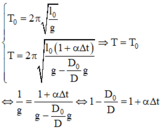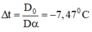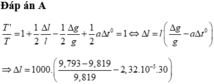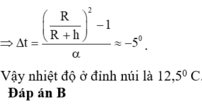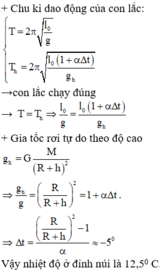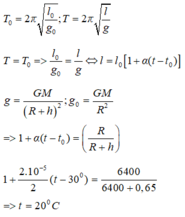Một con lắc đồng hồ có hệ số nở dài của dây treo con lắc α = 2 . 10 - 5 K - 1 Vật nặng có khối lượng riêng là D = 8700 kg/m3. Biết đồng hồ chạy đúng trong không khí có khối lượng riêng D0 = 1,3 kg/m3 ở nhiệt độ 250C. Nếu đồng hồ đặt trong hộp chân không mà vẫn đúng thì nhiệt độ ở trong hộp chân không xấp xỉ là (Trong không khí vật chịu thêm lực đẩy Acsimet)
A. 21,250C.
B. 28,750C.
C. 32,50C.
D. 17,50C.