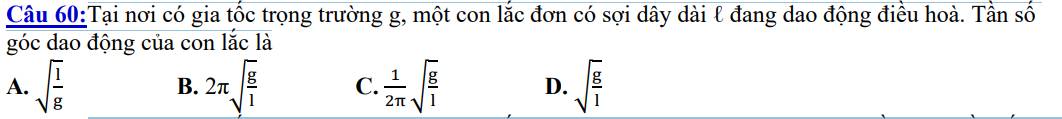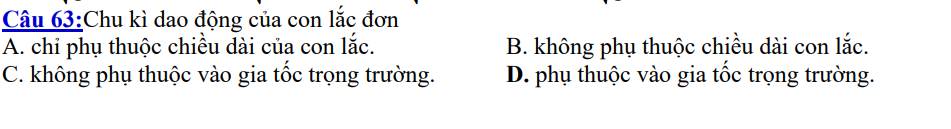
Bài 3. Con lắc đơn
Vật nhỏ dao động điều hoà dọc theo trục Ox với pt x=8cos(πt+π/2). Kể từ thời điểm t=0 vật cách vị trí cân bằng 4cm lần thứ 2021 ở thời điểm nào
Giải chi tiết giúp mình với ạ
Ta có `505T` thì `2020` lần vật đi qua vị trí cách vị trí cân bằng `4 cm`.
`=>\Delta t_[2021]=t_1 +505T=T/12 +505T`
`=6061/12 T=6061/12 .[2\pi]/[\pi]=6061/6 (s)`.
Đúng 2
Bình luận (0)
chu kì dao động một con lắc đơn tăng thêm 20% thì chiều dài con lắc sẽ phải A. tăng 22% B. giảm 44% C. tăng 20% D. tăng 44%
Xem chi tiết
Ta có: \(\dfrac{T'}{T}=\dfrac{2\pi\sqrt{\dfrac{l'}{g}}}{2\pi\sqrt{\dfrac{l}{g}}}=\sqrt{\dfrac{l'}{l}}=\dfrac{1,2T}{T}=1,2\Rightarrow l'=1,44l\)
\(\Rightarrow\dfrac{l'-l}{l}100\%=\dfrac{1,44l-l}{l}100\%=44\%\)
Chọn D
Đúng 4
Bình luận (0)
Các con lắc đơn có chiều dài lần lượt l1, l2, l3 = l1 + l2, L4 = l1 - l2 dao động với chu kỳ T1, T2, T3 = 2,4s, T4 = 0,8s. Chiều dài l1 và l2 nhận giá trị
Ta có: \(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow l=\dfrac{T\sqrt{g}}{2\pi}\)
Theo đề: \(\left\{{}\begin{matrix}l_3=l_1+l_2\\l_4=l_1-l_2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}l_1=\dfrac{l_3+l_4}{2}\\l_2=\dfrac{l_3-l_4}{2}\end{matrix}\right.\)
Ta có: \(l_1=\dfrac{\sqrt{g}\left(T_3+T_4\right)}{4\pi}=0,8\)
\(l_2=\dfrac{g\left(T_3^2-T_4^2\right)}{8\pi^2}=0,64\)
Đúng 2
Bình luận (0)
Trong khoảng thời gian t, con lắc có chiều dài l thực hiện được 12dđ. Nếu giảm chiều dài của con lắc 16cm thì trong khoảng thời gian t như trên, con lắc thực hiện được 20dđ. Chiều dài của con lắc là
A. 20cm
B. 25cm
C. 40cm
D. 50cm
Ta có: \(\left\{{}\begin{matrix}T=2\pi\sqrt{\dfrac{l}{g}}=\dfrac{t}{12}\\T'=2\pi\sqrt{\dfrac{l-16}{g}}=\dfrac{t}{20}\end{matrix}\right.\)
\(\Rightarrow\sqrt{\dfrac{l-16}{l}}=\dfrac{12}{20}\)
\(\Rightarrow l=25cm\)
Chọn B
Đúng 3
Bình luận (0)
Con lắc đơn dao động tại nơi có g = 10m/s^2 với biên độ góc 0,1 rad. Khi qua vị trí cân bằng con lắc có vận tốc 50cm/s. Chiều dài dây treo con lắc là?
Ở VTCB: \(\left|v\right|=\sqrt{2gl\left(cos\alpha-cos\alpha_0\right)}=\sqrt{2gl\left(1-cos\alpha_0\right)}\)
\(\Rightarrow l=2,5m\)
Đúng 3
Bình luận (0)
Con lắc đơn có chiều dài l = 0,64m, dao động điều hòa tại nơi có g = 10m/s^2. Lúc t = 0, con lắc qua vị trí cân bằng theo chiều dương của quỹ đạo với vận tốc 0,4m/s. Sau 2s vận tốc con lắc là?
Ta có: \(\omega=\sqrt{\dfrac{g}{l}}=\dfrac{5\pi}{4}\left(\dfrac{rad}{s}\right)\)
\(\rightarrow A=\dfrac{v_{max}}{\omega}=\dfrac{0,4}{\dfrac{5\pi}{4}}=\dfrac{8\pi}{25}\left(m\right)\)
\(t:0\left\{{}\begin{matrix}x=0\\v>0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{\pi}{2}\left(rad\right)\)
\(\rightarrow v=-4sin\left(\dfrac{5\pi}{4}t-\dfrac{\pi}{2}\right)\left(\dfrac{m}{s}\right)\)
Thay t = 2 vào \(\Rightarrow v=0\left(\dfrac{m}{s}\right)\)
Đúng 1
Bình luận (0)
Hai con lắc đơn có chiều dài lần lượt là l1 và l2 thì chu kì dđ tương ứng là T1 và T2. Nếu con lắc có chiều dài bằng l1 + l2 thì chu kì dđ của con lắc là 2,7s. Nếu con lắc có chiều dài bằng l1 - l2 thì chu kì dd0 của con lắc là 0,9s. Chu kì T1 và T2 là?
\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow T^2\) tỉ lệ thuận với l
Theo bài ra
\(\left\{{}\begin{matrix}T_1^2+T_2^2=\left(2,7\right)^2=7,29\\T_1^2-T_2^2=\left(0,9\right)^2=0,81\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}T_1^2=4,05\\T_2^2=3,24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}T_1=2,01s\\T_2=1,8s\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ở cùng một nơi trên trái đất con lắc đơn có chiều dài l1 dao động với chu kỳ T1 = 2s chiều dài l2 dao động với chu kỳ T2 = 1,5s. Tính chu kỳ dao động của con lắc đơn có chiều dài l1 + l2A. 6sB. 2,5sC. 2sD. 3,5s
Xem chi tiết
\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow T\) tỉ lệ thuận với \(\sqrt{l}\) => \(T^2\) tỉ lệ thuận với l
=> Con lắc đơn có chiều dài l=l1+l2 thì có chu kì \(T=\sqrt{T_1^2+T_2^2}=\sqrt{2^2+\left(1,5\right)^{^2}}=2,5s\)
=> Chọn B
Đúng 1
Bình luận (0)