Cho các tập hợp:
M = { x ∈ ℝ : x ≥ − 3 } , N = { x ∈ ℝ : − 2 ≤ x ≤ 1 } , P = { x ∈ ℝ : − 5 < x ≤ 0 } .
Mệnh đề nào sau đây là mệnh đề đúng?
A. M ⊂ N
B. M ⊃ P
C. N ⊂ M
D. N ⊂ P
Cho hai tập hợp A = { x ∈ ℝ : − 7 ≤ x ≤ 3 } , B = { x ∈ ℝ : − 1 < x < 5 } .
Tập hợp A ∩ B là:
A. ( − 1 ; 3 )
B. [ − 1 ; 3 )
C. ( − 1 ; 3 ]
D. ( 3 ; 5 )
Cho tập hợp M = ( - 2 ; 3 ] ; N = x ∈ ℝ : 1 x - 5 > 1 3 ; P = [ 1 ; + ∞ ) .
Tập hợp (M \ N) ∪ CRP là:
A. (-2; 1).
B. (-∞; 1 ).
C. (-∞ ; 2].
D. (-2; 2].
Đáp án: C
1 x - 5 > 1 3 ⇔ x - 5 < 3 ⇔ - 3 < x - 5 < 3 ⇔ 2 < x < 8 ⇒ N = ( 2 ; 8 ) . M \ N = ( - 2 ; 2 ] ; C ℝ P = ℝ \ P = ( - ∞ ; 1 ) ( M \ N ) ∪ C ℝ P = ( - ∞ ; 2 ] .
Cho điểm M( x ; y) có :
x = - 1 + 2 cos t y = 2 - 2 sin t ( t ∈ ℝ )
Tập hợp điểm M là:
A. Đường tròn tâm I( 1 ; -2) , bán kính R= 2.
B. Đường tròn tâm I( -1 ;2) , bán kính R= 2.
C. Đường tròn tâm I( -1 ; 2), bán kính R= 4.
D. Đường tròn tâm I( 1; -2) , bán kính R= 4.
Đáp án B
Ta có:
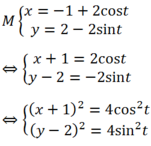
=> ( x +1) 2+ (y- 2) 2= 4cos2t + 4sin2t
=> ( x +1) 2+ (y- 2) 2 = 4
Vậy tập hợp điểm M là phương trình đường tròn có tâm I( -1;2) , bán kính R= 2.
Cho hai tập hợp A = ( − ∞ ; 1 ] , B = { x ∈ ℝ : − 3 < x ≤ 5 } . Tập hợp A ∩ B là:
A. ( − 3 ; 1 ]
B. [ 1 ; 5 ]
C. ( 1 ; 5 ]
D. ( − ∞ ; 5 ]
Ta có B = x ∈ R : − 3 < x ≤ 5 = − 3 ; 5
khi đó A ∩ B = − 3 ; 1
Đáp án A
Cho các tập P = [ - 1 ; + ∞ ) ; Q = x ∈ ℝ : 1 x - 2 > 1 .
Tập hợp (P ∪ Q) \ (P ∩ Q) là:
A. [– 1; 1] ∪ [3; +∞).
B. [– 1; 1) ∪ (3; +∞).
C. (1; 3).
D. [– 1; +∞).
Đáp án: A
1 x - 2 > 1 ⇔ x - 2 < 1 ⇔ - 1 < x - 2 < 1 ⇔ 1 < x < 3 ⇒ Q = ( 1 ; 3 ) ( P ∩ Q ) = ( 1 ; 3 ) ; ( P ∪ Q ) = [ - 1 ; + ∞ ) ( P ∪ Q ) \ ( P ∩ Q ) = [ - 1 , 1 ] ∪ [ 3 ; + ∞ ) .
Cho hai tập hợp A = { x ∈ ℝ : x − 2 ≤ 2 x } , B = { x ∈ ℝ : 4 x − 2 < 3 x + 1 } . Tập hợp các số tự nhiên thuộc cả hai tập A và B là:
A. ∅
B. { 0 ; 1 }
C. { 0 ; 1 ; 2 }
D. { 0 ; 1 ; 2 ; 3 }
Cho tập hợp A = (-∞; m] và B = {x ∈ R : (x2 + 1)(x - 2) > 0. Giá trị của m để A ∪ B = ℝ là
A. m > 0
B. m ≥ 2
C. m ≥ 0
D. m > 2
Đáp án: B
( x2 + 1)(x - 2) > 0 ⇔ x - 2 > 0 (do x2 + 1 > 0 ∀x ∈ R)
⇔ x > 2 => B = (2; ∞ ).
Để A ∪ B = R thì m ≥ 2
Cho hàm số f x có đạo hàm trên ℝ thỏa mãn f x + h - f x - h ≤ h 2 , ∀ x ∈ ℝ , ∀ h > 0 .Đặt g x = x + f ' x 2019 + x + f ' x 29 - m - m 4 - 29 m 2 + 100 sin 2 x - 1 , m là tham số nguyên mà m < 27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g (x) đạt cực tiểu tại x = 0. Tính tổng bình phương các phần tử của S.
A. 108
B. 58
C. 100
D. 50
Cho hàm số y = 1 3 x 3 + 2 x 2 + ( m + 2 ) x - m . Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên ℝ
A. S = ( - ∞ ; 2 ]
B. S = ( - ∞ ; 2 )
C. S = [ 2 ; + ∞ )
D. S = ( 2 ; + ∞ )