Thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC=2a bằng
PB
Những câu hỏi liên quan
Thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC 2a bằng A.
8
a
3
27
B.
8
a
3
3
3
C.
3
a
3
3
D. ...
Đọc tiếp
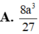
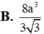
Thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC= 2a bằng
A. 8 a 3 27
B. 8 a 3 3 3
C. 3 a 3 3
D. 2 a 3 2
Đáp án D
Ta có cạnh của khối lập phương A B = A C 2 = a 2 ⇒ V = A B 3 = 2 a 3 2 .
Đúng 0
Bình luận (0)
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết
A
C
a
3
A.
V
a
3
B.
V
a
3
4
C.
V
3
6
a
3
4
D.
V...
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết A C ' = a 3
A. V = a 3
B. V = a 3 4
C. V = 3 6 a 3 4
D. V = 3 3 a 3
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC a
3
A
.
V
a
3
B
.
V
a
3
4
C
.
V
3
6...
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC' = a 3
A . V = a 3
B . V = a 3 4
C . V = 3 6 a 3 4
D . V = 3 3 a 3
Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có 
.
Do đó 
Đúng 0
Bình luận (0)
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết đường chéo
A
C
a
3
A.
a
3
3
B.
3
3
a
3
C.
3
6
a
3
4
D.
a...
Đọc tiếp
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết đường chéo A C ' = a 3
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’ biết
A
B
a
;
A
D
2
a
;
A
C
a
14
là A.
V
6
a
3
B.
V
a
3
14...
Đọc tiếp
Thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’ biết A B = a ; A D = 2 a ; A C ' = a 14 là
A. V = 6 a 3
B. V = a 3 14 3
C. V = a 3 5
D. V = 2 a 3
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là A.
4
a
3
3
B.
8
a
3
3
C.
2
a
3
3
D.
8...
Đọc tiếp
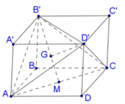
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
A. 4 a 3 3
B. 8 a 3 3
C. 2 a 3 3
D. 8 a 3 9
Đáp án B
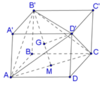
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C’ có
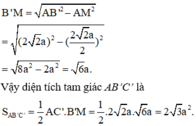
Xét tam giác vuông D’GB’ ta có
Đúng 0
Bình luận (0)
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
Đọc tiếp
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
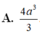
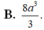
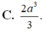
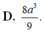
Chọn B
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C’ có
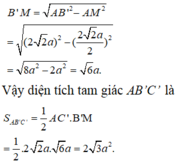
Xét tam giác vuông D’GB’ ta có
Đúng 0
Bình luận (0)
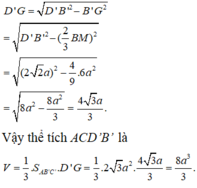
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’=4a, AC=2a, BD=a. Thể tích V của khối lăng trụ là
A. 8 a 3
B. 2 a 3
C. 8 3 a 3
D. 4 a 3
Cho hình lập phương ABCD.A’B’C’D’ cạnh 2a, gọi M là trung điểm của BB’ và P thuộc cạnh DD’ sao cho
D
P
1
4
D
D
. Mặt phẳng (AMP) cắt CC’ tại N. Thể tích khối đa diện AMNPBCD bằng A.
V
2
a
3
B.
V
3
a
3
C.
V
9
4...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh 2a, gọi M là trung điểm của BB’ và P thuộc cạnh DD’ sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC’ tại N. Thể tích khối đa diện AMNPBCD bằng
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 4 a 3
D. V = 11 3 a 3