Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()
Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()
Thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC=2a bằng
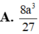
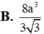
![]()
![]()
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, SA = 3 . Tính thể tích V của khối chóp S.ABC
A . V = 35 a 3 24
B . V = 3 a 3 6
C . V = 2 a 3 6
D . V = 2 a 3 2
Tính thể tích V của khối chóp đều S.ABC có cạnh đáy bằng 2a và cạnh bên bằng a 3
A . V = a 3 3
B . V = a 3 5 3
C . V = a 3 5
D . V = a 3 3 3
Cho hình chóp S.ABCD có cạnh bên SA = a (0 <a < 3 )và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
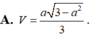
B. Đáp án khác.
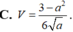
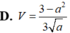
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
Cho khối nón có bán kính đáy r = 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()
Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a 3 là được thiết diện là hình vuông có diện tích bằng 4 a 2 Tính thể tích V của khối trụ (T)?.
![]()
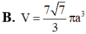

![]()
Cho khối nón có bán kính đáy r= 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()