Biết phương trình z 2 + a z + b = 0 ( b , c ∈ R ) có một nghiệm z=1-i. Tính môđun của số phức w=a+bi.
![]()
![]()
![]()
![]()
Biết phương trình z 2 + a z + b = 0 có một nghiệm là z = - 2 + i Tính a+b
A. 9
B. 1
C. 4
D. -1
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Đáp án D
Thay z=-2+i vào phương trình ta được:
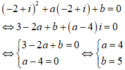
Vậy a-b=4-5=-1
Cách khác. Nghiệm liên hợp của nghiệm z 1 = - 2 + i là z 2 = - 2 - i
Ta có ![]() nên
z
1
,
z
2
là nghiệm của phương trình
nên
z
1
,
z
2
là nghiệm của phương trình ![]()
Do đó suy ra ![]()
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z=-2+i. Tính a+b
A. 9
B. 1
C. 4
D. -1
Đáp án A
Suy ra được nghiệm còn lại là
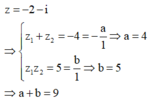
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z = -2 + i. Tính a + b
A. 9.
B. 1.
C. 4
D. -1
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ R ) có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
![]()
![]()
![]()
![]()
Biết phương trình z 2 + a z + b = 0 với a, b thuộc R có một nghiệm z = 1- 2i. Tính a +b
A. 1
B. -5
C. -3
D. 3
Biết phương trình z 2 + a z + b = 0 với a, b thuộc R có một nghiệm z = 1+ 2i. Giá trị a + b bằng
A. 1
B. -5
C. -3
D. 3
Tìm các số thực a,b,c để phương trình (ẩn z) z 3 + a z 2 + b z + c = 0 nhận z = 1 + i và z = 2 làm nghiệm
![]()
![]()
![]()
![]()