hãy cho biết tên hàm xác định giá trị nhỏ nhất và lớn nhất
LN
Những câu hỏi liên quan
em hãy cho biết tên hàm tìm giá trị nhỏ nhất và cú pháp của hàm tìm giá trị nhỏ nhất
tên hàm tính giá trị nhỏ nhất là MIN.
Đúng 0
Bình luận (0)
Em hãy nêu cú pháp của hàm tính tổng tính trung bình cộng xác định giá trị lớn nhất giá trị nhỏ nhất
- Hàm tính tổng: SUM
- Hàm tính trung bình cộng: AVERAGE
- Hàm xác định giá trị lớn nhất: MAX
- Hàm xác định giá trị nhỏ nhất: MIN
Đúng 0
Bình luận (0)
Trung bình cộng : =AVERAGE(A1;A2)
Gía trị lớn nhất: =MAX(A1;A2)
Gía trị bé nhất: =MIN(A1;A2)
Đúng 0
Bình luận (0)
Giúp mk vs, mai mk thy ùicâu 1:Hãy nêu cách chọn 1 ô? 1 cột ? 1 hàng? 1 khối?Câu 2;A/Viết công thức và cho biết chức năng của hàm tính tổng?B/Viết công thức và cho biết chức năng của hàm tính trung bình cộng?C/Viết công thức và cho biết chức năng của hàm xác định giá trị lớn nhất?D/Viết công thức và cho biết chức năng của hàm xác định giá trị nhỏ nhất?
Đọc tiếp
Giúp mk vs, mai mk thy ùi
câu 1:Hãy nêu cách chọn 1 ô? 1 cột ? 1 hàng? 1 khối?
Câu 2;A/Viết công thức và cho biết chức năng của hàm tính tổng?
B/Viết công thức và cho biết chức năng của hàm tính trung bình cộng?
C/Viết công thức và cho biết chức năng của hàm xác định giá trị lớn nhất?
D/Viết công thức và cho biết chức năng của hàm xác định giá trị nhỏ nhất?
Chọn 1 ô: đưa con trỏ chuột tới ô đó và nháy chuột
Chọn 1 cột: Nháy chuột tại nút tên cột
Chọn 1 hàng: Nháy chuột tại nút tên hàng
Chọn 1 khối: Kéo thả chuột từ 1 ô góc đến ô ở góc đối diện
Ví dụ
Ô A1 có chứa dữ liệu số là 8, ô A2 có chứa dữ kiệu số là 10
A/ =Sum(A1,A2) nhấn Enter
B/ =Average(A1,A2) nhấn Enter
C/ =Max(A1,A2) nhấn Enter
D/ =Min(A1,A2) nhấn Enter
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |
b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Đúng 4
Bình luận (0)
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |
b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Đúng 2
Bình luận (0)
tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2x²+10x+3/ - 3x² + 2x + 1 trên tập xác định là?
Cho hàm số yf(x) xác định và liên tục trên
−
1
;
5
2
và có đồ thị là đường cong như hình vẽ. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
f
x
trên
−
1
;
5
2
là A.
M...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên − 1 ; 5 2 và có đồ thị là đường cong như hình vẽ. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x trên − 1 ; 5 2 là
A. M = 4, m = 1.
B. M = 7 2 , m = 1.
C. M = 4, m = − 1.
D. M = 7 2 , m = − 1.
Đáp án C
Nhìn vào đồ thị ta thấy giá trị lớn nhất của hàm số trên − 1 ; 5 2 là M = 4 khi x = 5 2 . Giá trị nhỏ nhất của hàm số trên − 1 ; 5 2 là m = − 1 khi x = x C T . Vậy ta chọn C.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
xác định, liên tục trên
-
1
;
5
2
và có đồ thị là đường cong như hình vẽ.Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
f
x
trên
-
1
;
5
2...
Đọc tiếp
Cho hàm số y = f x xác định, liên tục trên - 1 ; 5 2 và có đồ thị là đường cong như hình vẽ.
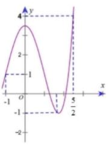
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x trên - 1 ; 5 2 là:
A. M = 4 , m = 1
B. M = 4 , m = - 1
C. M = 7 2 , m = - 1
D. M = 7 2 , m = 1
Cho hàm số
y
f
(
x
)
xác định và liên tục trên
ℝ
, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số
y
f
(
x
)
trên đoạn
-
2
;
2
. A. m -5, M 0 B. m -5, M -1 C. m -1, M 0 D. m -2,...
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f ( x ) trên đoạn - 2 ; 2
.
A. m = -5, M = 0
B. m = -5, M = -1
C. m = -1, M = 0
D. m = -2, M = 2
Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.
Đúng 0
Bình luận (0)