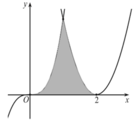
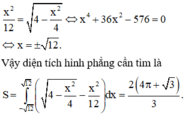Diện tích hình phẳng giới hạn bởi parabol y= ( x - 2 ) 2 , đường cong y= x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
A. 11 2
B. 73 12
C. 7 12
D. 5 2
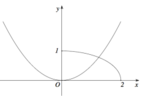
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 đường cong y = 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên).
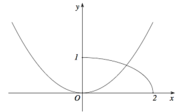
Diện tích của (H) bằng
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3
Diện tích hình phẳng giới hạn bởi parabol y = x - 2 2 , đường cong y = x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
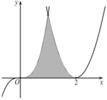
A. 11 2
B. 73 12
C. 7 12
D. 5 2
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 , đường cong 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 đường cong 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng
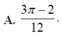
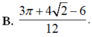
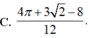
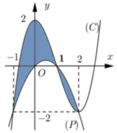
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
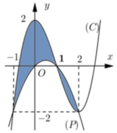
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 − x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
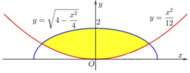
A. 2 4 π + 3 3
B. 4 π + 3 6
C. 4 3 + π 6
D. 4 π + 3 3
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (hình vẽ). Diện tích của hình phẳng (H) bằng
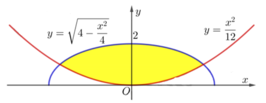
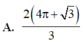
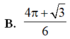
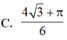
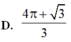
Cho hình phẳng (H) giới hạn bởi Parabol y = x 2 12 và đường cong có phương trình y = 4 - x 2 4 (như hình vẽ). Diện tích của hình phẳng (H) bằng
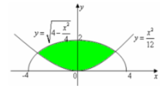
A. 4 π + 3 3
B. 4 3 + π 6
C. 4 π + 3 6
D. 2 4 π + 3 3
Chọn D.
Phương pháp: Tìm cận và dùng tích phân để tính diện tích.
Cách giải: Ta có phương trình hoành độ giao điểm là