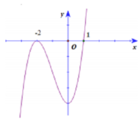
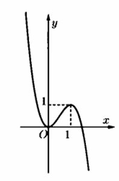
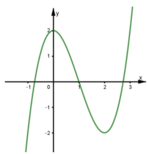
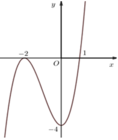
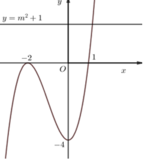
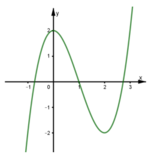
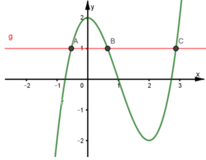
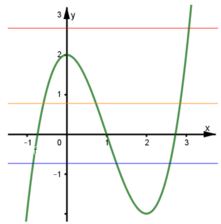
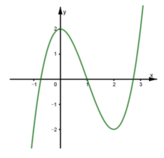
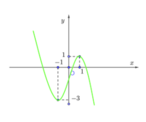
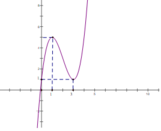
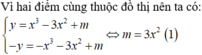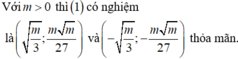Cho hàm số y=f(x) có đồ thị như hình sau. Số nghiệm của phương trình
1
-
f
(
x
)
1
+
f
(
x
)
=
2
là: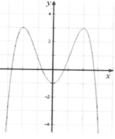
![]()
![]()
![]()
![]()