Nghiệm của phương trình
z
2
+
2
z
+
5
0
là
Đọc tiếp
Nghiệm của phương trình z 2 + 2 z + 5 = 0 là
PB
Những câu hỏi liên quan
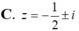
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
A. 3.
B. 2.
C. 4.
D. 1.
Chọn C.
Gọi z = a + bi là nghiệm của phương trình.
Ta có: 4(a + bi) 2 + 8(a2 + b2) - 3 = 0
4(a2 – b2 + 2abi) + 8( a2 + b2) - 3 = 0
12a2 + 4b2 +8abi - 3 = 0
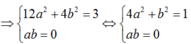
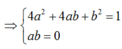
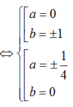
Vậy phương trình có 4 nghiệm phức.
Đúng 0
Bình luận (0)
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
Nếu z1-i và z1 là 2 nghiệm của phương trình thì
a
-
b
-
c
bằng A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Biết
z
1
,
z
2
là 2 nghiệm phức của phương trình:
2
z
2
-
(
3
-
1
)
z
+
5
0
. Chọn khẳng định đúng
A
.
z
1
.
z
2...
Đọc tiếp
Biết z 1 , z 2 là 2 nghiệm phức của phương trình: 2 z 2 - ( 3 - 1 ) z + 5 = 0 . Chọn khẳng định đúng
A . z 1 . z 2 = 1
B . z 1 = z 2 ¯
C . z 1 2 = z 2 2
D . z 1 = - z 2
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
2
và
z
1
+
i
làm các nghiệm của phương trình. Khi đó
a
-
b
+
c
là
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) 0 trên tập số phức, tính tổng: A. 2/5 B. 3/5 C. 5/4 D. 6/7
Đọc tiếp
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: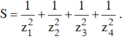 
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
Đúng 0
Bình luận (0)
Tổng các nghiệm của phương trình
z
+
i
1
+
i
3
-
z
2
-
1
+
2
i
z
2...
Đọc tiếp
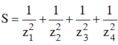
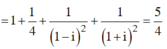
Tổng các nghiệm của phương trình z + i 1 + i 3 - z 2 - 1 + 2 i z 2 i + 2 = 0 là:
A. 1 + 2i
B. 2 - i
C. 1 - 2i
D. 2 + i
Đáp án C
Ta có z 2 - 1 + 2 i z = z 2 + 2 i z + i 2 = z + i 2 . Đặt w = z + i , khi đó phương trình đã cho trở thành:
w 3 1 + i 3 - w 2 2 i + 2 = 0 ⇔ w 3 - 1 + i w 2 - 4 + 4 i = 0 ⇔ w - 2 w - 2 i w + 1 + i = 0 [ w = 2 w = 2 i w = - 1 - i ⇔ [ z + i = 2 z + i = 2 i z + i = - 1 - i ⇔ [ z = 2 - i z = i z = - 1 - 2 i ⇒ ∑ z = 2 - i + i - 1 - 2 i = 1 - 2 i .
Đúng 0
Bình luận (0)
z
1
+
i
là một nghiệm của phương trình
x
2
+
b
x
+
2
0
. Tìm b A. – 1 B. 2 C. – 2 D. 1
Đọc tiếp
z = 1 + i là một nghiệm của phương trình x 2 + b x + 2 = 0 . Tìm b
A. – 1
B. 2
C. – 2
D. 1
z
1
+
i
là một nghiệm của phương trình
x
2
+
b
x
+
2
0
. Tìm b
Đọc tiếp
z = 1 + i là một nghiệm của phương trình x 2 + b x + 2 = 0 . Tìm b
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
3
z
2
-
z
+
2
0
. Tính
|
z
1
|
2
+
|
z
2
|
2
A. -11/9 B. 8/3 C. 2/3 D. 4/3
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính | z 1 | 2 + | z 2 | 2
A. -11/9
B. 8/3
C. 2/3
D. 4/3
