Cho số phức z và w thỏa mãn z + w = 3 + 4 i và z - w = 9 Tìm giá trị lớn nhất của biểu thức T = z + w
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn |z| = 5 và số phức w = ( 1 + i ) z Tìm |w|
A. 10
B. 2 + 5
C. 5
D. 2 5
Đáp án A
Phương pháp: Cho z1, z2 là hai số phức bất kì, khi đó | z1.z2 | = |z1|.|z2|
Cách giải: Ta có:
![]()
![]()
Số phức z thỏa mãn z = 5 và số phức w = ( 1 + i ) z ¯ Tìm w
A. 10
B. 2 + 5
C. 5
D. 2 5
Đáp án A
Phương pháp: Cho
z
1
,
z
2
là hai số phức bất kì, khi đó ![]()
Cách giải: Ta có:
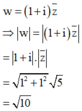
Các số phức z, w thay đổi nhưng thỏa mãn |z + i – 2i| = 1 và |w - 3 + i| = 3. Tìm |z - w|max
A. |z - w|max = 2.
B. |z - w|max = 4.
C. |z - w|max = 9.
D. |z - w|max = 10.
Cho số phức z thỏa mãn z + 1 - i = z - 3 i và số phức w = 1 z . Tìm giá trị lớn nhất của w .
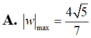
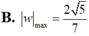
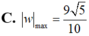
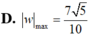
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i
Cho các số phức z và w thỏa mãn ( 3 - i ) | z | = z w - 1 + 1 - i . Tìm GTLN của T = | w + i |
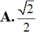
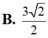
![]()
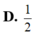
Cho các số phức z và w thỏa mãn ( 3 - i ) z = z w - 1 + 1 - i . Tìm GTLN của T = w + i .
A. 2 2
B. 3 2 2
C. 2
D. 1 2
Cho số phức z và w thỏa mãn z+w=3+4i và z - w = 9 .
Tìm giá trị lớn nhất của biểu thức T = z + w .
A. maxT= 176
B. maxT=14
C. maxT=4
D. maxT= 106
Đáp án D
Đặt ![]() theo giả thiết ta có:
theo giả thiết ta có:
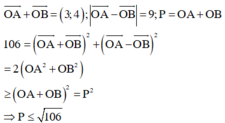
Tổng quát: Với 2 số thực
z
1
,
z
2
thõa mãn ![]()
Khi đó ![]()
Cho số phức z thỏa mãn: |z|= 4. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (3+4i)z + i là một đường tròn có bán kính là:
A. 4.
B. 5.
C. 20.
D. 22.
Đáp án C
Đặt ![]() Số phức w được biểu diễn bởi điểm M (x;y).
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
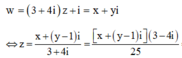
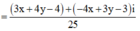
=> |z| = 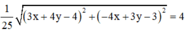
![]()
![]()
![]()
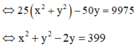
![]()
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: ![]()