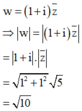Đáp án A
Phương pháp: Cho
z
1
,
z
2
là hai số phức bất kì, khi đó ![]()
Cách giải: Ta có: