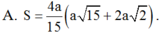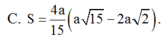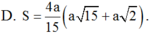Cho hình chóp SABC có A B = α , B C = α 3 , A B C ^ = 30 ° Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp SABC bằng

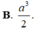
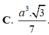
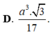
Cho hình chóp tam giác đều SABC có chiều cao α , cạnh bên bằng 2 α . Tính thể tích V của khối chóp SABC
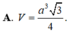
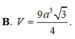

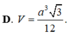
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , AC=b, AB=c, B A C ^ = α . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c, α .
![]()
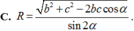
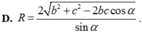
Hình chóp SABC, đáy ABCD là hình bình hành; (α) là mặt phẳng chứa A và trung điểm M của SC, (α) // BD. Biết (α) chia SABCD thành 2 phần có thể tích V1, V2 (V1 là thể tích bé hơn). Tính V 1 V 2
A. V 1 V 2 = 1.
B. V 1 V 2 = 1 2 .
C. V 1 V 2 = 1 3 .
D. V 1 V 2 = 1 4 .
cho hình chóp SABCD có ABCD là hình thang vuông tại A và B với AB = BC = a , AD = 2a ; SA ⊥ ( ABCD ) và SA = 2a . Gọi M là 1 điểm nằm trên AB ; (α) là mặt phẳng qua M , vuông góc với AB . Đặt x=AM ( 0< x < α ) .
a, Tìm thiết diện của hình chóp với (α) . Thiết diện là hình gì ?
b, Tính diện tích thiết diện theo a và x
dạ giúp mình bài này với ạ , mình cảm ơn ạ
Gọi N, Q lần lượt là trung điểm của AB , CD \(\Rightarrow\left\{{}\begin{matrix}MN\perp AB\\MQ\perp AB\end{matrix}\right.\)
Qua N kẻ đường thẳng song song với BC , cắt SC tại P
suy ra thiết diện của mặt phẳng (\(\alpha\) ) và hình chóp là MNPQ
Vì MQ là đường t/b của hình thang ABCD , \(\Rightarrow MQ=\dfrac{3a}{2}\)
MN là đường t/b của tam giác SAB; \(MN=\dfrac{SA}{2}=a\)
NP là đường t/b của tam giác SBC ; \(\Rightarrow NP=\dfrac{BC}{2}=\dfrac{a}{2}\)
Vậy diện tích hình thang MNPQ là : \(S_{MNPQ}=\dfrac{MN.\left(NP+MQ\right)}{2}=\dfrac{a}{2}.\left(\dfrac{a}{2}+\dfrac{3a}{2}\right)=a^2\)
Cho hình chóp SABC có đáy là tam giác đều cạnh α , SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600. Thể tích của khối chóp SABC bằng
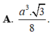
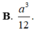
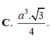
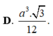
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
, AC = b, AB = c, ![]() . Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c,
α
.
. Gọi B', C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp hình chóp A.BCC'B' theo b, c,
α
.
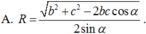
![]()
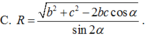
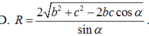
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng (α).
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
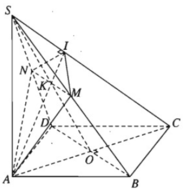
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 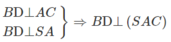
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
Cho hình chóp S.ABCD có đáy ABC vuông tại B, (SAC) vuông góc với (ABC), biết SB = SC = a , SA = BC = a 3 . Gọi α là góc tạo bởi SA và (SBC). Tính sin α
A. sin α = 2 13
B. sin α = 3 13
C. sin α = 1 3 13
D. sin α = 1 2 13
Chọn A.
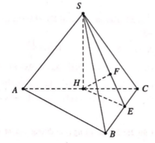
Dựng SH ⊥ AC , do ( SAC ) ⊥ ( ABC ) nên SH ⊥ ( ABC ) ; AC = 2 a . Dựng HE ⊥ BC ; HF ⊥ SE ⇒ d ( H ; ( SBC ) ) = HF . ΔSAC = ΔBCA ⇒ ΔSAC vuông tại S .
Dễ thấy tan ACB ^ = 1 3 ⇒ ACB ^ = 30 o = SAC ^ HC = SCcos 60 o = a 2 ; HE = HCsin 30 o = a 4 ; SH = a 3 2 . Do AC = 4 HC ⇒ d A = 4 d H = 4 . SH . HE SH 2 + HE 2 = 2 39 13 Do đó Sinα = d A SA = 2 13 .
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng ( α ) song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d ( B , ( α ) ) = a 2 và A B = a 2 .