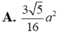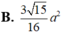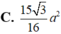cho hình chóp SABCD có ABCD là hình thang vuông tại A và B với AB = BC = a , AD = 2a ; SA ⊥ ( ABCD ) và SA = 2a . Gọi M là 1 điểm nằm trên AB ; (α) là mặt phẳng qua M , vuông góc với AB . Đặt x=AM ( 0< x < α ) .
a, Tìm thiết diện của hình chóp với (α) . Thiết diện là hình gì ?
b, Tính diện tích thiết diện theo a và x
dạ giúp mình bài này với ạ , mình cảm ơn ạ
Gọi N, Q lần lượt là trung điểm của AB , CD \(\Rightarrow\left\{{}\begin{matrix}MN\perp AB\\MQ\perp AB\end{matrix}\right.\)
Qua N kẻ đường thẳng song song với BC , cắt SC tại P
suy ra thiết diện của mặt phẳng (\(\alpha\) ) và hình chóp là MNPQ
Vì MQ là đường t/b của hình thang ABCD , \(\Rightarrow MQ=\dfrac{3a}{2}\)
MN là đường t/b của tam giác SAB; \(MN=\dfrac{SA}{2}=a\)
NP là đường t/b của tam giác SBC ; \(\Rightarrow NP=\dfrac{BC}{2}=\dfrac{a}{2}\)
Vậy diện tích hình thang MNPQ là : \(S_{MNPQ}=\dfrac{MN.\left(NP+MQ\right)}{2}=\dfrac{a}{2}.\left(\dfrac{a}{2}+\dfrac{3a}{2}\right)=a^2\)