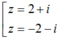Cho z = 1 - i . Tìm căn bậc hai dạng lượng giác của z:
A. 2 4 cos - π 8 + i . sin - π 8 v à 2 4 cos 7 π 8 + i . sin 7 π 8
B. 2 cos π 4 + i . sin π 4
C. 2 cos - π 4 + i . sin - π 4
D. 2 4 cos π 8 + i . sin π 8 v à 2 4 cos - π 8 + i . sin - π 8
Cho z = 1 - i. Tìm căn bậc hai dạng lượng giác của z:
A. 2 4 cos - π 8 + i sin - π 8 v à 2 4 cos 7 π 8 + i sin 7 π 8
B. 2 cos π 4 + i sin π 4
C. 2 cos - π 4 + i sin - π 4
D. 2 4 cos π 8 + i sin π 8 v à 2 4 cos - π 8 + i sin - π 8
Các bạn giải giúp mình nha!
Câu 1: Tìm tất cả các số nguyên x=>y=>z=>0 sao cho:
xyz + xy+ yz + xz +x+y+z=2011
Câu 2 Giải phương trình :
4(x^2+2)^2 = 25(x^3+1)
Câu 3 Tìm Max ,Min của
P= 2x^2 - xy - y^2
Với x, y thỏa mãn: x^2 + 2xy+ 3y^2=4
Câu 4 Cho a,b,c là độ dài ba cạnh của tam giác chứng minh:
1/(a^2+bc) + 1/(b^2+ac)+1/(c^2+ab) <= (a+b+c)/(2abc)
Câu 5 Tìm các số hữu tỉ x,y thỏa mãn:
x(căn bậc hai của(2011) + căn bậc hai của(2010)) + y(căn bậc hai của(2011) - căn bậc hai của(2010)) = Căn bậc hai của(2011^3) + Căn bậc hai của(2010^3)
cho A=căn bậc hai của x-3/2. tìm x thuộc Zvà x<30 để A có giá trị nguyên
cho B=5/căn bậc hai của x-1. tìm x thuộc Z để B có giá trị nguyên
cho x,y,z là các số thực thỏa mãn -1<=x,y,z <=1 và x+y+z =o. tìm GTNN biểu thức :P=căn bậc 2 1+x+y^2 +căn bậc 2 của 1+y+z^2 + căn bậc 2 của 1+z+x^2
căn bậc 2 của (x) +căn bậc 2 của (y)+căn bậc 2 của (z)=2 ; x+y+z=2 tính P= căn bậc 2 của ((x+1)(y+1)(z+1)) ((căn bậc 2 của (x) /(x+1))+(căn bậc 2 của (y) / (y+1))+(căn bậc 2 của (z) / (z+1))
căn bậc 2 của (x) +căn bậc 2 của (y)+căn bậc 2 của (z)=2 ; x+y+z=2 .tính P= căn bậc 2 của ((x+1)(y+1)(z+1)) ((căn bậc 2 của (x) /(x+1))+(căn bậc 2 của (y) / (y+1))+(căn bậc 2 của (z) / (z+1))
Cho z = 3 + 4 i . Tìm căn bậc hai của z.
A. -2 + i và 2 - i
B. 2 + ivà 2 - i
C. 2 + i và -2 - i
D. 3 + 2 i v à - 3 - 2 i
Chọn C.
Giả sử w = x + yi(x, y ∈ R) là một căn bậc hai của số phức z = 3 + 4i.
Ta có:
![]()
![]()
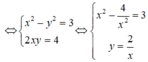
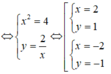
Do đó z có hai căn bậc hai là
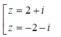
Cho z = 3 + 4i. Tìm căn bậc hai của z ?
A. -2 + i và 2 - i
B. 2 + i và 2 - i
C. 2 + i và -2 - i
D. 3 + 2 i v à - 3 - 2 i
Chọn C.
Giả sử w = x + yi (x,y ∈ R) là một căn bậc hai của số phức z = 3 + 4i.
Ta có:
![]()
![]()
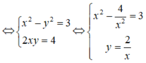
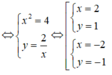
Do đó z có hai căn bậc hai là z = 2 + i hoặc z = -2 - i.
Cho z = 3 + 4i. Tìm căn bậc hai của z.
A. -2 + i và 2 - i
B. 2 + i và 2 - i
C. 2 + i và -2 - i
D. 3 - 2i và 2 - 3i
Chọn A.
Giả sử w = x + yi là một căn bậc hai của số phức z = 3 + 4i.
Ta có:
![]()
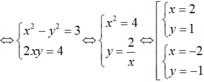
Do đó z có hai căn bậc hai là