Tìm họ nguyên hàm
∫
(
2
x
+
1
)
e
x
d
x
Đọc tiếp
Tìm họ nguyên hàm ∫ ( 2 x + 1 ) e x d x
PB
Những câu hỏi liên quan
Tìm họ nguyên hàm của hàm số
y
1
(
x
+
1
)
2
A.
∫
1
(...
Đọc tiếp
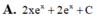
Tìm họ nguyên hàm của hàm số y = = 1 ( x + 1 ) 2
A. ∫ 1 ( x + 1 ) 2 d x = - 2 ( x + 1 ) 3 + C
B. ∫ 1 ( x + 1 ) 2 d x = - 1 x + 1 + C
C. ∫ 1 ( x + 1 ) 2 d x = 1 x + 1 + C
D. ∫ 1 ( x + 1 ) 2 d x = 2 ( x + 1 ) 3 + C
Đáp án B
Phương pháp: Sử dụng công thức ∫ 1 ( a x + b ) 2 = - 1 a ( a x + b ) + C
Cách giải: ∫ 1 ( x + 1 ) 2 d x = - 1 x + 1 + C
Đúng 0
Bình luận (0)
1/(x+1)^2 tìm họ nguyên hàm
Lời giải:
\(\int \frac{1}{(x+1)^2}dx=\int \frac{1}{(x+1)^2}d(x+1)=-\frac{1}{x+1}+C\)
Đúng 0
Bình luận (0)
Tìm họ nguyên hàm F(x) của hàm số
f
(
x
)
x
3
+
x
+
1
.
A.
F
(
x
)
x
4
4
+
x
3
2
+
C
B.
F
(...
Đọc tiếp
Tìm họ nguyên hàm F(x) của hàm số f ( x ) = x 3 + x + 1 .
A. F ( x ) = x 4 4 + x 3 2 + C
B. F ( x ) = x 4 4 + x 3 2 + x + C
C. F ( x ) = x 4 + x 3 2 + x + C
D. F ( x ) = 3 x 3 + C
Tìm họ nguyên hàm F(x) của hàm số
f
(
x
)
x
3
+
x
+
1
. A.
F
(
x
)
:
x
4
4
+
x
3
2
+
C
B.
F
(
x
)
:
x...
Đọc tiếp
Tìm họ nguyên hàm F(x) của hàm số f ( x ) = x 3 + x + 1 .
A. F ( x ) : x 4 4 + x 3 2 + C
B. F ( x ) : x 4 4 + x 2 2 + x + C
C. F ( x ) : x 4 + x 3 2 + x + C
D. F ( x ) : 3 x 3 + C
Tìm họ nguyên hàm F(x) của hàm số
f
(
x
)
x
3
+
x
+
1
Đọc tiếp
Tìm họ nguyên hàm F(x) của hàm số f ( x ) = x 3 + x + 1
Tìm họ nguyên hàm của hàm số
f
(
x
)
x
2
–
x
+
1
x
-
1
. A.
x
+
1
x
+
1
+
C
B.
x...
Đọc tiếp
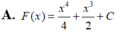
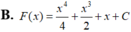
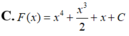
Tìm họ nguyên hàm của hàm số f ( x ) = x 2 – x + 1 x - 1 .
A. x + 1 x + 1 + C
B. x + 1 x + 1 2 + C
C. x 2 2 + ln x - 1 + C
D. x 2 + ln x - 1 + C
Tìm họ nguyên hàm F(x) của hàm số
f
x
x
3
+
x
+
1
A.
F
x
x
4
4
+
x
3
2
+
C
B.
F
x...
Đọc tiếp
Tìm họ nguyên hàm F(x) của hàm số f x = x 3 + x + 1
A. F x = x 4 4 + x 3 2 + C
B. F x = x 4 4 + x 3 2 + x + C
C. F x = x 4 + x 3 2 + x + C
D. F x = 3 x 2 + C
Tìm họ nguyên hàm của hàm số
f
(
x
)
x
2
-
x
+
1
x
-
1
Đọc tiếp
Tìm họ nguyên hàm của hàm số f ( x ) = x 2 - x + 1 x - 1
Tìm họ nguyên hàm của hàm số
f
(
x
)
x
2
−
x
+
1
x
−
1
A.
x
+
1
x
−...
Đọc tiếp
Tìm họ nguyên hàm của hàm số f ( x ) = x 2 − x + 1 x − 1
A. x + 1 x − 1 + C
B. 1 + 1 ( x − 1 ) 2 + C
C. x 2 2 + ln x − 1 + C
D. x 2 + ln x − 1 + C
Đáp án C
Có f x = x + 1 x − 1
Nguyên hàm của f(x) là F x = x 2 2 + ln x − 1 + C .
Đúng 0
Bình luận (0)
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{5\sin x}{2\sin x-\cos x+1}\)
Biến đổi :
\(5\sin x=a\left(2\sin x-\cos x+1\right)+b\left(2\cos x+\sin x\right)+c\)
= \(\left(2a+b\right)\sin x+\left(2b-a\right)\cos x+a+c\)
Đồng nhất hệ số hai tử số :
\(\begin{cases}2a+b=5\\2b-a=0\\a+c=0\end{cases}\)
\(\Rightarrow\) \(\begin{cases}a=2\\b=1\\c=-2\end{cases}\)
Khi đó :
\(f\left(x\right)=\frac{2\left(2\sin x-\cos x+1\right)+\left(2\cos x+\sin x\right)-2}{2\sin x-\cos x+1}\)
= \(2+\frac{2\cos x+\sin x}{2\sin x-\cos x+1}-\frac{2}{2\sin x-\cos x+1}\)
Do vậy :
\(I=2\int dx+\int\frac{\left(2\cos x+\sin x\right)dx}{2\sin x-\cos x+1}-2\int\frac{dx}{2\sin x-\cos x+1}\)
=\(2x+\ln\left|2\sin x-\cos x+1\right|-2J+C\)
Với
\(J=\int\frac{dx}{2\sin x-\cos x+1}\)
Đúng 0
Bình luận (0)