5 d m 2 2 c m 2 = . . . . . . c m 2
Số điền vào chỗ chấm là
A. 502
B. 5002
C. 520
D. 5200
Tìm M nằm trên △: x+2y-2=0, biết:
a) AM=5, A(2;-1)
b) d(M,ox)=\(\sqrt{2}\)
c) d(M,oy)=\(\sqrt{3}\)
d) d(M,ox) = d(M,oy)
b: Ox: y=0
=>0x+y+0=0
M thuộc Δ nên M(-2y+2;y)
\(d\left(M;\text{Δ}\right)=\dfrac{\left|\left(-2y+2\right)\cdot0+y\cdot1+0\right|}{\sqrt{0^2+1^2}}=\sqrt{2}\)
=>|y|=căn 2
=>y=căn 2 hoặc y=-căn 2
=>\(M\left(2-2\sqrt{2};\sqrt{2}\right)\) hoặc \(M\left(2+2\sqrt{2};-\sqrt{2}\right)\)
c: Oy: x=0
=>x+0y+0=0
x+2y-2=0
=>2y=-x+2
=>y=-0,5x+1
=>M(x;-0,5x+1)
d(M;Oy)=căn 3; M(x;-0,5x+1); x+0y+0=0(Oy)
=>\(\dfrac{\left|x\cdot1+\left(-0.5x+1\right)\cdot0+0\right|}{\sqrt{1^2+0^2}}=\sqrt{3}\)
=>\(\left|x\right|=\sqrt{3}\)
=>\(\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\)
=>\(M\left(\sqrt{3};\dfrac{2-\sqrt{3}}{2}\right)\) hoặc \(M\left(-\sqrt{3};\dfrac{2+\sqrt{3}}{2}\right)\)
Bài 1:
a) C/m: A=2^1+2^2+2^3+2^4+....+2^2010 chia het cho 3 và 7
b) C/m: B=3^1+3^2+3^3+3^4+....+3^2010 chia het cho 4 va 13
c) C/m: C= 5^1+5^2+5^3+5^4+....+5^2010 chia het cho 6 va 31
d) C/m: D=7^1+7^2+7^3+7^4+....+7^2010 chia het cho 8 va 57
1. Cho a+5/a-5/b+6/b-6(a khác 5, b khác 6). C/m rằng a/b=5/6.
2.C/m rằng nếu a/b=c/d thì a^2+b^2/c^2+d^2=a.b/c.d.
Đồ thị của hàm số y = (-2)/5x là đường thẳng OM. Khi đó:
(A) M(-5; 2)
(B) M(2; -5)
(C) M((-2)/5; 1)
(D) M((-6)/5; 3)
Xét hàm số 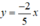 , với x = -5 thì
, với x = -5 thì 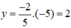 nên điểm M(-5; 2) thuộc đồ thị hàm số
nên điểm M(-5; 2) thuộc đồ thị hàm số 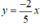
Vậy đồ thị của hàm số 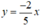 là đường thẳng OM với M(-5; 2).
là đường thẳng OM với M(-5; 2).
Đáp số (A)
1. bất phương trình \(\frac{3x+5}{2}-1\le\frac{x+2}{3}+x\) có bao nhiêu nghiệm nguyên lớn hơn -10
A.4 B.5 C.9 D.10
2. tổng các nghiệm của bất phương trình x(2-x) ≥ x(7-x) - 6(x-1) trên đoạn \([-10;10]\)
A. 5 B.6 C.21 D.40
3. tập nghiệm S của bất phương trình 5( x+1) - x( 7-x) > -2x
A. R B. \(\left(-\frac{5}{2};+\infty\right)\) C.\(\left(-\infty;\frac{5}{2}\right)\) D. ϕ
4. Tập nghiệm S của bất phương trình x+\(\sqrt{x}< \left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)\)
A. (-∞;3) B. (3; +∞) C. [3; +∞) D. (-∞; 3]
5. tổng các nghiệm nguyên của bất phương trình \(\frac{x-2}{\sqrt{x-4}}\le\frac{4}{\sqrt{x-4}}\) bằng
A. 15 B. 26 C. 11 D. 0
6. bất phương trình (m2- 3m )x + m < 2- 2x vô nghiệm khi
A. m ≠1 B. m≠2 C. m=1 , m=2 D. m∈ R
7. có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 -m )x < m vô nghiệm
A. 0 B.1 C.2 D. vô số
8. gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phương trình (m2 -m)x + m< 6x -2 vô nghiệm. tổng các phần tử trong S là
A. 0 B.1 C.2 D.3
9. tìm tất cả các giá trị thực của tham số m để bất phương trình m2( x-2) -mx +x+5 < 0 nghiệm đúng với mọi x∈ [-2018; 2]
A. m< \(\frac{7}{2}\) B. m= \(\frac{7}{2}\) C. m > \(\frac{7}{2}\) D. m ∈ R
10. tìm tất cả các giá trị thực của tham số m để bất phương trình m2 (x-2) +m+x ≥ 0 có nghiệm x ∈ [-1;2]
A. m≥ -2 B. m= -2 C. m ≥ -1 D. m ≤ -2
Cho hàm số y=(2-m)x +m+1 với m là tham số và m # 2 có đồ thị là đg thẳng d
b, tìm m để d cắt đg thẳng y =2x-5 tại điểm có hoành độ =2
c, tìm m để d cùng vs trục tọa độ Ox , Oy tạo thành 1 tam giác có S =2
b: Thay x=2 vào y=2x-5, ta được:
y=2*2-5=-1
Thay x=2 và y=-1 vào (d), ta được:
2(2-m)+m+1=-1
=>4-2m-m+1=-1
=>-3m+5=-1
=>m=2
c: Gọi A,B lần lượt là giao của (d) với trục Ox,Oy
=>\(A\left(\dfrac{-m-1}{2-m};0\right)\Leftrightarrow A\left(\dfrac{m+1}{m-2};0\right)\); OB(0;m+1)
=>OA=|m+1|/|m-2|; OB=|m+1|
Theo đề, ta có: 1/2*OA*OB=2
=>(m+1)^2/|m-2|=4
TH1: m>2
Pt sẽ là m^2+2m+1=4(m-2)=4m-8
=>m^2-2m+9=0(loại)
TH2: m<2
Pt sẽ là m^2+2m+1=4(2-m)=8-4m
=>m^2+6m-7=0
=>(m+7)(m-1)=0
=>m=1 hoặc m=-7
Hàm số \(\dfrac{x+2}{x-m+2}\) xác định trên (1; 3) khi:
A. m < 3 B. m ≥5 C. m < 3 hoặc m > 5 D. m ≥ 5 hoặc m ≤ 3.
Các bạn làm giúp mình ba bài này nha
Bài 1. Chứng minh rằng
A) ( a - b ) + ( c - d )- ( a + c ) = - (b + d)
B) ( a - b ) - ( c- d) + ( b + c) = a + d
C) a (b-c) -b ( a-c) = c ( b-a)
D) b (c-a) + a( b - c ) =c(b-a)
E) -c (-a +b) + b ( c-a) = a (c-b)
G) a ( c - b) - b ( -a - c) = c( a + b)
Bài 2. Tìm số nguyên n biết:
A) (2n + 9 ) M(n - 1)
B) (5 - n) M(n - 2)
C) (10- 3n) M(n - 1)
D) (n2 - n - 5) M( n - 1)
E) (2n 2 + 5n + 5) M ( n - 2)
G) ( n2 - 5) M ( n + 1)
Bài 3. Tìm giá trị nhỏ nhất của các biểu thức A, C, E
A= (x-2)2+3
C=x2 + (y-3)2-1
E=(3x-3)2 + 2.|y+1|-1
Bài 1:
a) Ta có: (a-b)+(c-d)-(a+c)
=a-b+c-d-a-c
=-b-d(1)
Ta lại có: -(b+d)=-b-d(2)
Từ (1) và (2) suy ra (a-b)+(c-d)-(a+c)=-(b+d)
b) Ta có: (a-b)-(c-d)+(b+c)
=a-b-c+d+b+c
=a+d(đpcm)
c) Ta có: a(b-c)-b(a-c)
=ab-ac-ab+cb
=cb-ca
=c(b-a)(đpcm)
d) Ta có: b(c-a)+a(b-c)
=bc-ba+ab-ac
=bc-ac
=c(b-a)(đpcm)
e) Ta có: -c(-a+b)+b(c-a)
=ca-cb+bc-ba
=ca-ba
=a(c-b)(đpcm)
g) Ta có: a(c-b)-b(-a-c)
=ac-ab+ba+bc
=ac+bc
=c(a+b)(đpcm)
Hàm số y = x 4 + ( m 2 - 4) x 2 + 5 có ba cực trị khi:
A. -2 < m < 2 B. m = 2
C. m < -2 D. m > 2
Đáp án: A.
Hàm số y = x 4 + ( m 2 - 4) x 2 + 5 có 3 cực trị khi y' = 0 có 3 nghiệm phân biệt, tức là
y' = 4 x 3 + 2( m 2 - 4) = 2x(2 x 2 + m 2 - 4) = 0 có ba nghiệm phân biệt
⇔ 2 x 2 + m 2 - 4 = 0 có hai nghiệm phân biệt khác 0.
⇔ 4 - m 2 > 0 ⇔ -2 < m < 2.
Hàm số y = x 4 + ( m 2 - 4) x 2 + 5 có ba cực trị khi:
A. -2 < m < 2 B. m = 2
C. m < -2 D. m > 2
Đáp án: A.
Hàm số y = x 4 + ( m 2 - 4) x 2 + 5 có 3 cực trị khi y' = 0 có 3 nghiệm phân biệt, tức là
y' = 4 x 3 + 2( m 2 - 4) = 2x(2 x 2 + m 2 - 4) = 0 có ba nghiệm phân biệt
⇔ 2 x 2 + m 2 - 4 = 0 có hai nghiệm phân biệt khác 0.
⇔ 4 - m 2 > 0 ⇔ -2 < m < 2.