Giusp mình với PLS
NH
Những câu hỏi liên quan
Giusp mình đi Pls💦
Tìm tất cả các STN có 2 chữ số sao cho số đó cộng với số viết theo thứ tự ngược lại cho ta một số chính phương.
Giusp mình với ạ. Mình đang cần gấp. Pls
\(\overline{ab}+\overline{ba}=11\left(a+b\right)\)
11 là số nguyên tố để 11(a+b) là số chính phương thì a+b=11
\(\Rightarrow\overline{ab}=\left\{29;38;47;56;65;74;83;92\right\}\)
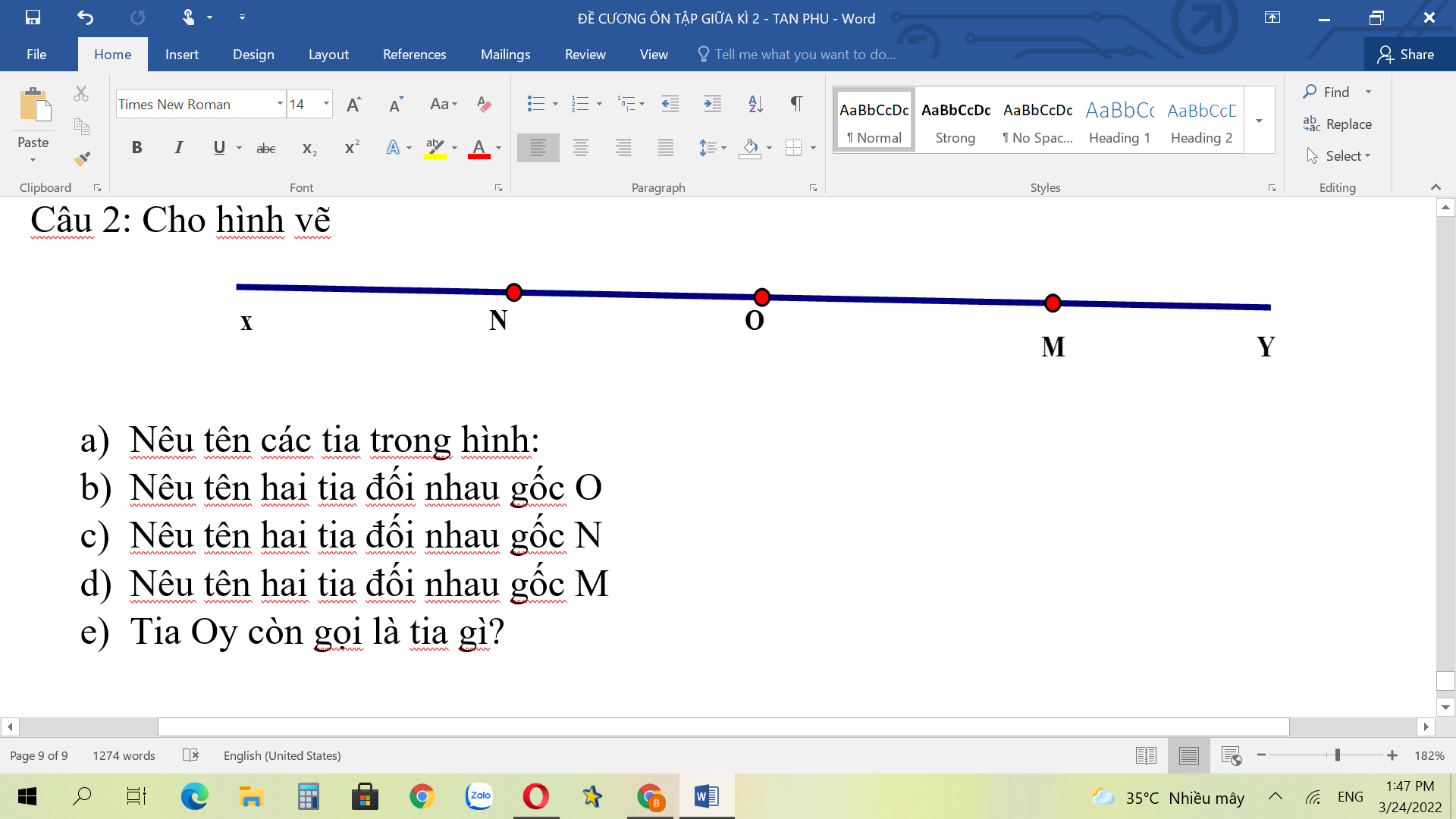
Giusp Mình với ạ ,mình cảm ơn nhiều
a: xN,xO,xO,xM,NO,NM,Nx,My,MO
b: ON và OM
c; NO và Nx
d: Mx và My
e: Còn gọi là tia OM
Đúng 0
Bình luận (0)
Giusp mình với ạ


Giusp mình với ạ

Giusp mình với ạ !!

Giusp mình với ạ
Giusp mình với ạ!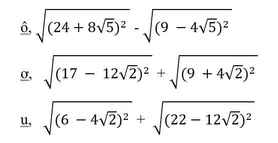
\(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}=24+8\sqrt{5}-9+4\sqrt{5}=15+12\sqrt{5}\)
\(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}=17-12\sqrt{2}+9+4\sqrt{2}=26-8\sqrt{2}\)
\(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}=6-4\sqrt{2}+22-12\sqrt{2}=28-16\sqrt{2}\)
Đúng 1
Bình luận (0)
\(ô,\\ \Rightarrow24+8\sqrt{5}-\sqrt{\left(9-4\sqrt{5}\right)^2}\\ \Rightarrow24+8\sqrt{5}-\left(9-4-\sqrt{5}\right)\\ \Rightarrow24+8\sqrt{5}-9+4\sqrt{5}\\ \Rightarrow15+8\sqrt{5}+4\sqrt{5}\\ \Rightarrow15+12\sqrt{5}\)
\(ơ,\\ g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4+\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+9+4\sqrt{2}\)
\(u,\\ 6-4\sqrt{2}+\sqrt{\left(22-12\sqrt{2}\right)}^2\\ \Rightarrow6-4\sqrt{2}+22-12\sqrt{2}\\ \Rightarrow28-4\sqrt{2}-12\sqrt{2}\\ \Rightarrow28-16\sqrt{2}\)
Đúng 0
Bình luận (1)
ô \(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}\)
= 24 + 8\(\sqrt{5}\) - 9 + 4\(\sqrt{5}\)
= 15 + 12\(\sqrt{5}\)
ơ \(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}\)
= 17 - 12\(\sqrt{2}\) + 9 + 4\(\sqrt{2}\)
= 26 - 8\(\sqrt{2}\)
u \(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}\)
= 6 - 4\(\sqrt{2}\) + 22 - 12\(\sqrt{2}\)
= 28 -16\(\sqrt{2}\)
Đúng 0
Bình luận (0)









