Cho hệ phương trình y = 2 x + 20 y = 2 m - 4 x + 10 . Tìm m để hệ phương trình đã cho vô nghiệm
A. m = 3
B. m = 1
C. m = -2
D. m = -1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
1) Giải hệ phương trình $\left\{\begin{array}{l}2 x+y=19 \\ 3 x-2 y=11\end{array}\right.$.
2) Giải phương trình $x^{2}+20 x-21=0$.
3) Giải phương trình $x^{4}-20 x^{2}+64=0$.
3(2x+y)-2(3x-2y)=3.19-11.2
6x+3y-6x+4y=57-22
7y=35
y=5
thay vào :
2x+y=19
2x+5=19
2x=14
x=7
2/ x2+21x-1x-21=0
x(x+21)-1(x+21)=0
(x+21)(x-1)=0
TH1 x+21=0
x=-21
TH2 x-1=0
x=1
vậy x = {-21} ; {1}
3/ x4-16x2-4x2+64=0
x2(x2-16)-4(x2-16)=0
(x2-16)-(x2-4)=0
TH1 x2-16=0
x2=16
<=>x=4;-4
TH2 x2-4=0
x2=4
x=2;-2
Bài 1 :
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}4x+2y=38\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}7x=49\\2x+y=19\end{cases}}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=7\\2x+y=19\end{cases}}\)Thay vào x = 7 vào pt 2 ta được :
\(14+y=19\Leftrightarrow y=5\)Vậy hệ pt có một nghiệm ( x ; y ) = ( 7 ; 5 )
Bài 2 :
\(x^2+20x-21=0\)
\(\Delta=400-4\left(-21\right)=400+84=484\)
\(x_1=\frac{-20-22}{2}=-24;x_2=\frac{-20+22}{2}=1\)
Bài 3 : Đặt \(x^2=t\left(t\ge0\right)\)
\(t^2-20t+64=0\)
\(\Delta=400+4.64=656\)
\(t_1=\frac{20+4\sqrt{41}}{2}\left(tm\right);t_2=\frac{20-4\sqrt{41}}{2}\left(ktm\right)\)
Theo cách đặt : \(x^2=\frac{20+4\sqrt{41}}{2}\Rightarrow x=\sqrt{\frac{20+4\sqrt{41}}{2}}=\frac{\sqrt{20\sqrt{2}+4\sqrt{82}}}{2}\)
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\hept{\begin{cases}6x+3y=57\\6x-4y=22\end{cases}\hept{\begin{cases}7y=35\\3x-2y=11\end{cases}}}}\)
\(\hept{\begin{cases}y=5\\3x-2.5=11\end{cases}\hept{\begin{cases}y=5\\3x=21\end{cases}\hept{\begin{cases}y=5\\x=7\end{cases}}}}\)
\(a=1,b=20;c=-21\)
\(\Delta=\left(20\right)^2-\left(4.1.-21\right)=484\)
\(\sqrt{\Delta}=\sqrt{484}=22\)
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-20+22}{2}=1\left(TM\right)\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=-21\left(TM\right)\)
\(3,x^4-20x^2+64=0\)
đặt \(x^2=a\)ta có pt
\(a^2-20a+64=0\)
\(a=1;b=-20;c=64\)
\(\Delta=\left(-20\right)^2-\left(4.1.64\right)=144\)
\(\sqrt{\Delta}=12\)
\(a_1=\frac{-b+\sqrt{\Delta}}{2a}=16\left(TM\right)\)
\(a_2=\frac{-b-\sqrt{\Delta}}{2a}=4\left(TM\right)\)
\(< =>x_1=\sqrt{16}=4\left(TM\right)\)
\(x_2=\sqrt{4}=2\left(TM\right)\)
vậy bộ n0 của pt là (\(4;2\))
cho hệ phương trình x + y = 3k - 2
2x - y = 5 với k là tham số
giải hệ phương trình khi k = 1
tìm k để hệ phương trình có nghiệm ( x ; y) sao cho x^2 - y - 5/ y + 1 = 4
Thay k=1 và HPT ta có:
\(\left\{{}\begin{matrix}x+y=3.1-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x+y=1\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\3y=-3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y) = (2;-1)
b) tìm k để hệ phương trình có nghiệm ( x ; y) sao cho \(x^2-y-\dfrac{5}{y}+1=4\)
\(\left\{{}\begin{matrix}x+y=3k-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-\left(3k-2-x\right)=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-3k+2+x=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\3x=3k+3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\x=k+1\end{matrix}\right.\)
Ta có \(\text{ x= k+1 }=>y=2k-3\) (*)
Thay vào biểu thức đã cho ở đề bài ta có :
\(x^2-y-\dfrac{5}{y}+1=4\)
⇔\(\left(k+1\right)^2-2k+3-\dfrac{5}{2k-3}+1=4\)
⇔\(k^2+2k+1-2k+3-\dfrac{5}{2k-3}+1=4\)
Sau một hồi bấm máy tính Casio thì ra k=2
Vậy k=2 thì Thỏa mãn yêu cầu đề bài
Lần sau bạn dùng Latex đánh đề bài cho dễ nhìn nha, mình sợ chép lại đề bài bị sai @@
Cho hệ phương trình ( x+y = 2 mx−y = m với m là tham số.
a) Giải hệ phương trình khi m = −2.
b) Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x; y) sao cho 3x−y = −10.
c) Tìm giá trị nguyên của m để hệ phương trình có nghiệm (x; y) mà x, y là những số nguyên
a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....
Cho hệ phương trình: 2X +Y = 3m-2 ( m là tham số ) X - Y = 5 a) Giải hệ phương trình khi m = - 4 ; b) Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn: x + y = 13.
cho hệ phương trình
\(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y+1\end{matrix}\right.\)
a)giải hệ phương trình khi m=2
b)giải hệ phương trình theo m
c)tìm m để hệ có nghiệm (x;y) là các số dương
d)tìm m để hệ phương trình có nghiệm thỏa mãn x^2+y^2=1
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
cho hệ phương trình {x+2y=2 , mx-y=m (m là tham số) a) giải hệ phương trình khi m=2 b) tìm m để hệ phương trình nhận cặp (x,y)=(2,-1) làm nghiệm
a, tại m=2 thì hệ tương đương với\(\hept{\begin{cases}x+2y=2\\2x-y=2\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\4x-2y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\5x=6\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}}}} }\)
b, do thay (x,y)=(2,-1) vào phương trình x+2y=2 không thỏa mãn nên hệ phương trình không nhận cặp (x,y)=(2,-1) là nghiệm
Cho hệ phương trình : x + a y = 3 a x - y = 2
c) Tìm giá trị của a để hệ phương trình có nghiệm (x; y) thỏa mãn x = 2 y
c) Hệ phương trình đã cho có nghiệm
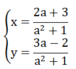
Theo đề bài : x= y
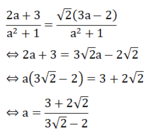
Vậy với 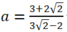 thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y
thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y
Cho hệ phương trình: a2x + y = 1 và x + y = a
a, giải hệ phương trình với a = -2
b, tìm các giá trị của a để hệ phương trình có vô số nghiệm
c, tìm a để hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x,y đều nguyên
Cho hệ phương trình x + my = 2m
x - y = m-1
giải hệ phương trình khi m = 2
tìm m để hệ có ngiệm duy nhất (x,y) thỏa mãn x^2 +2014y^2 = 2015
a, bạn tự giải
b, \(\left\{{}\begin{matrix}\left(m-1\right)y=m+1\\x=m-1+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{m+1}{m-1}\\x=\dfrac{m^2-2m+1+m+1}{m-1}=\dfrac{m^2-m+2}{m-1}\end{matrix}\right.\)
Thay vào ta được \(\left(\dfrac{m^2-m+2}{m-1}\right)^2+\dfrac{2014\left(m+1\right)}{m-1}=2015\)
bạn ktra lại đề nhé
Cho hệ phương trình 4 x - 3 y = 4 2 x + y = 2 . Biết nghiệm của hệ phương trình (x; y) , tính x.y
A. 2
B. 0
C. -2
D. 1