Cho hàm số y = x − 3 x − 2 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 1 ; + ∞
B. Hàm số nghịch biến trên từng khoảng xác định.
C. Hàm số nghịch biến trên R
D. Hàm số đồng biến trên từng khoảng xác định.
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)
Câu 48. Cho y=|x+1|+|x−2|và các mệnh đề
1)Hàm số tăng lên trên(-1,+∞)
2)Hàm số không đổi trên[−1;2)
3) Hàm số giảm trên(-∞,-1)
4) Hàm số giảm trên (-2,+∞)
Hỏi có bao nhiêu mệnh đề đúng?
A. 0 B. 1 C. 2 D. 3
Câu 49. Hàm số y=-√|2x+3|nghịch biến trên khoảng.
A.(\(-\dfrac{3}{2},+\infty\))
B.(-∞,\(-\dfrac{3}{2}\))
C. R
D.Cả 3 đáp án đều sai
Cho hàm số y=f(x)có đạo hàm y'= x 2 ( x - 2 ) . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên ![]() .
.
C. Hàm số nghịch biến trên ![]() và
và ![]()
D. Hàm số đồng biến trên ![]()
Ta có:
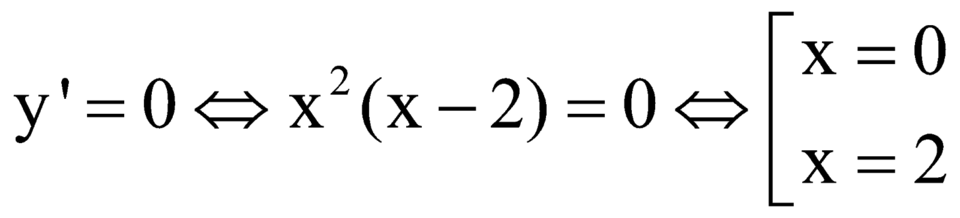
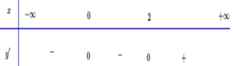
Dựa vào BBT ta thấy hàm số nghịch biến trên ![]() và đồng biến trên
và đồng biến trên ![]()
Chọn D.
Cho hàm số y = f(x) có đạo hàm y'= x 2 ( x - 2 ) . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên (0;2).
C. Hàm số nghịch biến trên ![]()
D. Hàm số đồng biến trên (2; + ∞ )
Cho hàm số y=f(x). Hàm số y= f’(x) có đồ thị như hình vẽ dưới đây.
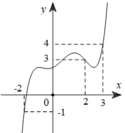
Đặt g ( x ) = 2 f ( x ) - x + 1 2 .Biết f(-2)=f(3). Mệnh đề nào đúng?
A. ![]()
B![]()
C. ![]()
D. ![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f(x) có đạo hàm f ' x = x + 1 2 2 - x x + 3 . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (-3;2)
B. Hàm số nghịch biến trên các khoảng - 3 ; - 1 v à 2 ; + ∞
C. Hàm số đồng biến trên các khoảng - ∞ ; - 3 v à 2 ; + ∞
D. Hàm số đồng biến trên khoảng (-3;2)
Đáp án D
Ta có: f ' x > 0 ⇔ - 3 < x < 2 f ' x < 0 ⇔ [ x > 2 x < - 3
Suy ra hàm số đồng biến trên khoảng (-3;2), nghịch biến trên các khoảng - ∞ ; - 3 v à 2 ; + ∞ .
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D=R\{3}.
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị.
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. 1,2,3.
B. 3,4.
C. 2,3,4.
D. 1,4.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
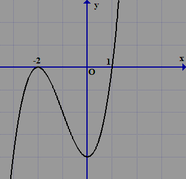
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Chọn D
Xét hàm số ![]() .
.
Có ![]()
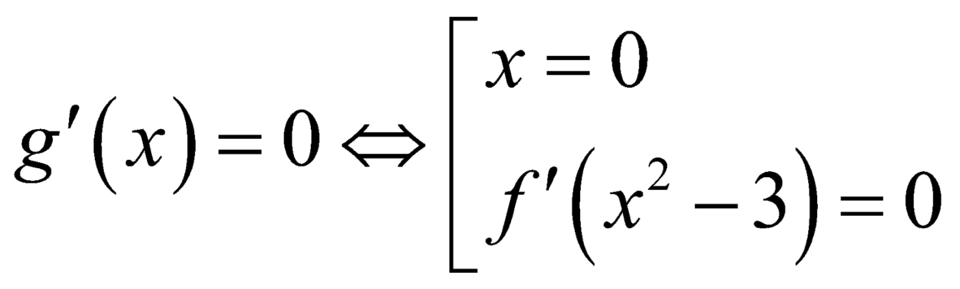
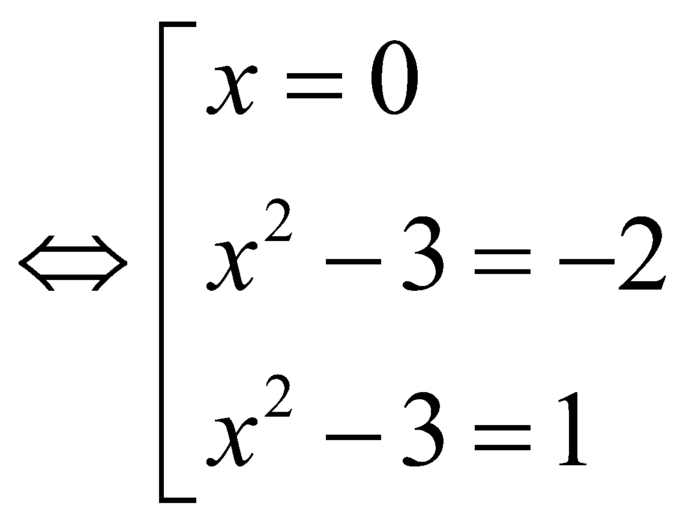
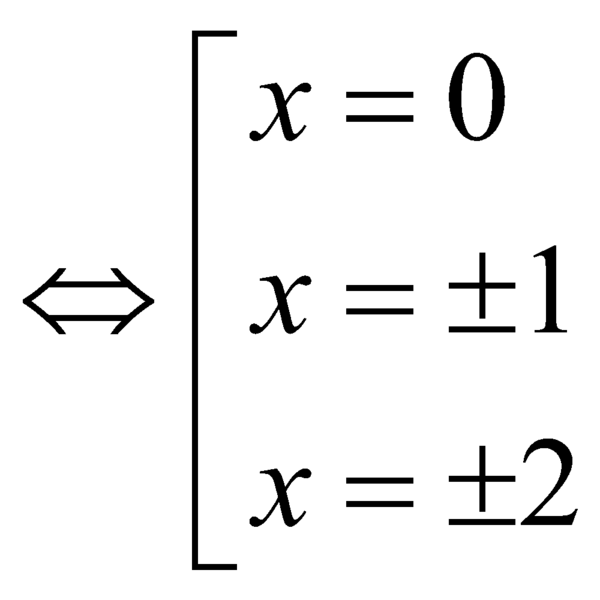 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
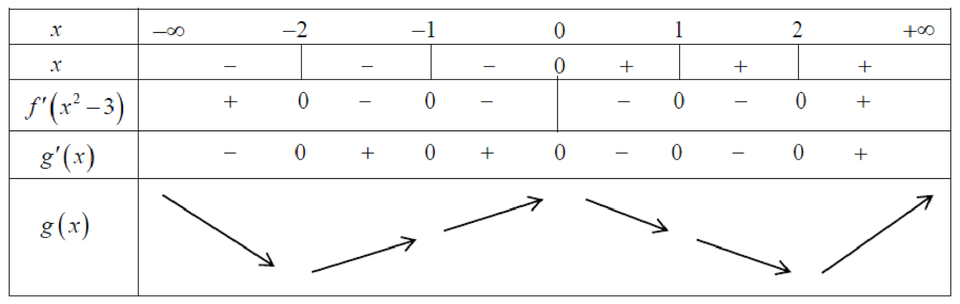
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????