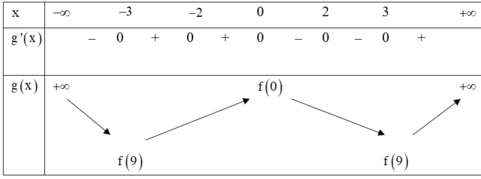
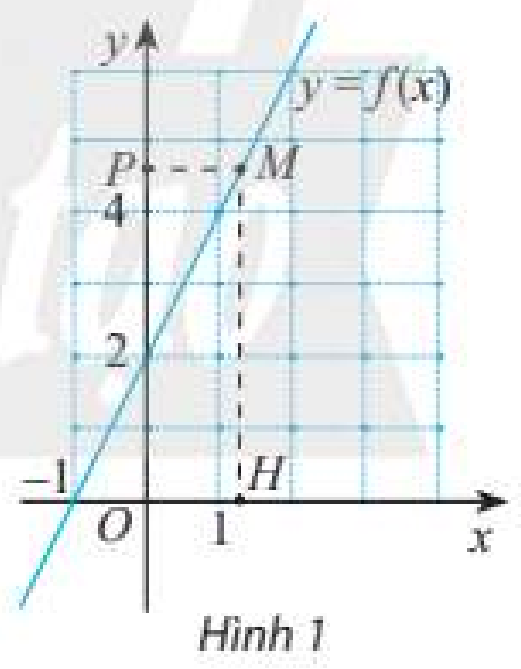
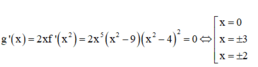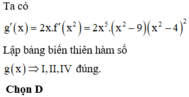Cho hàm số y = x − 2 x + 1 . Xét các phát biểu sau đây
+) Đồ thị hàm số nhận điểm I − 1 ; 1 làm tâm đối xứng.
+) Hàm số đồng biến trên tập ℝ \ − 1 .
+) Giao điểm của đồ thị với trục hoành là điểm A 0 ; − 2
+) Tiệm cận đứng là y = 1 và tiệm cận ngang là x = − 1
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 1
B. 3
C. 2
D. 4