Gọi H là hình chiếu vuông góc của S lên đáy

\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=60^0\)

\(\Rightarrow AH=BH=CH=\dfrac{SH}{tan60^0}\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác đáy

\(\Rightarrow AH=R=\dfrac{AB.BC.AC}{4S_{ABC}}\)

\(\Rightarrow SH=AH.tan60^0=\dfrac{AB.BC.AC.\sqrt{3}}{4S_{ABC}}\)

\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{AB.BC.CA.\sqrt{3}}{4S_{ABC}}.S_{ABC}=\dfrac{5a^3\sqrt{3}}{12}\)

\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)

Gọi H là hình chiếu vuông góc của S lên đáy

Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC

Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC

\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)

\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)

\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)

Đáp án B

Gọi M là trung điểm của BC   . Vì Δ A B C cân tại A nên  A M ⊥ B C   ,

Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C

->Góc giữa S B C và A B C là góc S M A  Vì góc  S A M = 90 0

Có B M = a , góc  B A M = 60 0   nên 

sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3

tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3

V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9

Đáp án B

Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC

Gọi M là trung điểm BC, do tam giác cân tại A \(\Rightarrow H\in AM\)

Kéo dài AM cắt đường tròn ngoại tiếp tam giác tại D \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn

\(\Rightarrow\Delta ABD\) vuông tại B

\(BM=\dfrac{1}{2}BC=\dfrac{3a}{2}\)  \(\Rightarrow AM=\sqrt{AB^2-BM^2}=\dfrac{a\sqrt{7}}{2}\)

Áp dụng hệ thức lượng:

\(AB^2=AM.AD\Rightarrow AD=\dfrac{AB^2}{AM}=\dfrac{8a\sqrt{7}}{7}\)

\(\Rightarrow AH=\dfrac{AD}{2}=\dfrac{4a\sqrt{7}}{7}\)

\(\Rightarrow SH=\sqrt{SA^2-AH^2}=\dfrac{2a\sqrt{21}}{7}\)

\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AM.BC=...\)

Đáp án là B

Đáp án là D

Hạ S D ⊥ ( A B C )  Ta có:

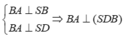
⇒ B A ⊥ D B ⇒ ∠ D B C = 60 ° Tương tự ta có

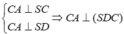
⇒ C A ⊥ D C ⇒ ∠ C D B = 60 °

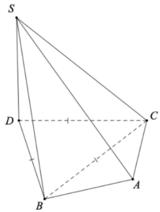
Do đó ∆ C B D đều cạnh

Vậy 

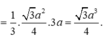
Chọn đáp án B.