Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
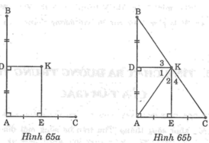
Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.
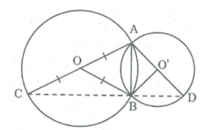
Nối AB, BO, BC, BO', BD.
* Trong ∆ ABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ∆ ABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ ∠ (ABC) = 90 0
* Trong ∆ ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))
Nên BO' là đường trung tuyến của tam giác ABD.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABD vuông tại B ⇒ ∠ (ABD) = 90 0
Ta có: ∠ (ABC) + ∠ (ABD) = ∠ (CBD) = 90 0 + 90 0 = 180 0
Vậy C, B, D thẳng hàng.
Cho hình vẽ Chứng minh ba điểm B K C thẳng hàng
Cho hình bình hành ABCD. Gọi H và K lần lượt là hình chiếu của A và C trên đường chéo BD.
a)v Chứng minh rằng DH = BK
b) Chứng minh rằng tứ giác AHCK là hình bình hành
c) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
nhanh 3 k miễn phí mai nhớ cổ vũ đội bóng việt nam nha
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.
c) AHCK là HBH =>2 đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của HK
=> O là trung điể của AC
=> A,O,C thẳng hàng
Cho hình 72. Trong đó ABCD là hình bình hành
a) Chứng minh rằng AHCK là hình bình hành
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
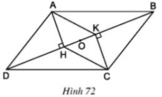
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.
Cho hình 88.
Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
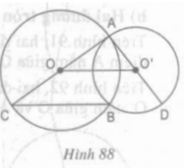
Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Cho hình 13.
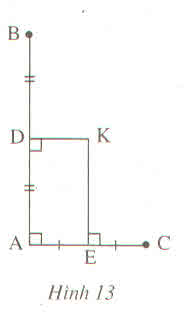
Chứng minh rằng ba điểm B, K, C thẳng hàng ?
Nối KA,KB,KC.
Ta có KD là đường trung trực AB
=>KA=KB(tính chất đường trung trực)
\(\Rightarrow\Delta KAB\) cân tại K nên KD là đường phân giác của \(\widehat{AKB}\)
\(\Rightarrow\widehat{K_1}=\widehat{K_3}\)
\(\Rightarrow\widehat{AKB}=2\widehat{K_1}\) (1)
KE là đường trung trực của AC
=>KA=KC(tính chất đường trung trực)
\(\Rightarrow\Delta KAC\) cân tại K nên KE là đường phân giác của \(\widehat{AKC}\)
\(\Rightarrow\widehat{K_2}=\widehat{K_4}\)
\(\Rightarrow\widehat{AKC}=2\widehat{K_2}\left(2\right)\)
\(KD\perp AB\left(gt\right)\)
\(AC\perp AB\left(gt\right)\)
Cho hình bình hành ABCD có E ,F lần lượt là trung điểm của AB,CD.Đường chéo BD cắt CE tại I a)chứng minh rằng AEGF là hình bình hành . b)gọi K là giao điểm của AC và BD chứng minh ba điểm E,K,E thẳng hàng và CL=2EL
Đề sai rồi, em ghi đề chính xác lại
Cho hình thang ABCD (AB//CD) gọi E , F , K lần lượt là trung điểm của Ad , AC , BC a) Chứng minh EF//CD b) Chứng minh EK//CD c) Chứng minh ba điểm E,F,K thẳng hàng
Cho hình bình hành ABCD (AB>AD) gọi E và K lần lượt là trung điểm của CD và AB, BD cắt AC tại O chứng minh rằng :
a, Tứ giác AECK là hình bình hành
b, ba điểm E,O,K thẳng hàng
a) Ta có: \(AB=DC,AB//CD\)(ABCD là hình bình hành)
Mà \(K,E\in AB,CD;AK=\dfrac{1}{2}AB;CE=\dfrac{1}{2}CD\)
\(\Rightarrow AK=CE\) và \(AK//CE\)
=> AECK là hình bình hành
b) Ta có: O là giao điểm 2 đường chéo AC và BD
=> O là trung điểm AC
=> O là trung điểm KE(AECK là hình bình hành)
=> E,O,K thẳng hàng